≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Задачи на букву З

Продолжение списка занимательные задачи (страница 8).

Задача о делении хлеба.
задача на прогрессию, старинная задача
Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Задача о жулике.
задача на вероятность, старинная задача
Однажды в Неаполе преподобный Галианн увидел человека, который встряхивал три игральные кости в чашке и держал пари, что выбросит три шестерки. Причем, делал это раз за разом, получая все больший куш. - Черт возьми! - вскричал преподобный Галианн. - Кости налиты свинцом! Так оно и оказалось. Какова же, на самом деле, вероятность выпадения трех шестерок?

Задача о зернах на шахматной доске.
задача на прогрессию, задача на шахматной доске, старинная задача
В старинной индийской легенде говорится о изобретателе шахмат, которому было предложено запросить любое вознаграждение за свое гениальное изобретение, на что он попросил положить на шахматную доску зерна пшеницы: на первую клетку одно зерно, на каждую следующую клетку в два раза больше зерен чем на предыдущую. Сколько всего зерен запросил мудрец?

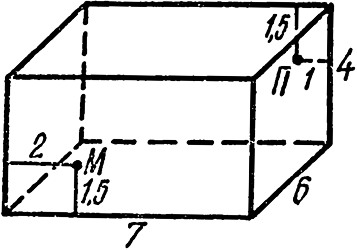
Задача о пауке и мухе.
старинная задача, геометрическая задача
На противоположных стенах комнаты определенной длины и ширины сидят муха и паук, муха - на полтора аршина от пола, паук - на полтора аршина от потолка. Какое между ними кратчайшее расстояние, которое мог бы проползти паук, чтобы достать муху?

Задача о подбрасывании двух игральных костей.
задача на вероятность
Великий математик и философ Готтфрид-Вильгельм Лейбниц (1646 - 1716) считал, что число 12 при бросании двух игральных костей выпадает также часто, как и число 11. Так ли это?

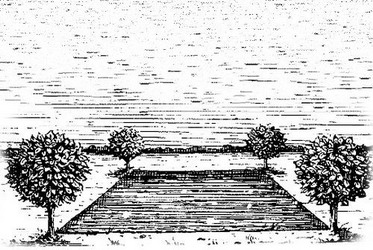
Задача о пруде.
геометрическая задача, задача на инвариант
Имеется квадратный пруд. По углам его, близ самой воды, растет 4 старых развесистых дуба. Пруд понадобилось расширить: сделать вдвое больше по площади, сохранив квадратную форму. Но вековые дубы трогать не хотят. Можно ли расширить пруд до требуемых размеров так, чтобы все 4 дуба, оставаясь на своих местах, оказались на берегах нового пруда?

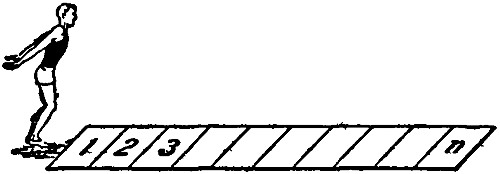
Задача о прыгуне.
комбинаторная задача, задача с перестановками
Сколькими, способами прыгун, стоящий перед клетками, начерченными на земле, может, достигнуть 10-й клетки, если он прыгает слева направо, приземляясь лишь в начерченных клетках, и длина его прыжков может быть произвольна?

Задача о путешественнике в пустыне.
старинная задача, задача на максимум и минимум
Необходимо найти максимальное расстояние, на которое может удалиться в пустыню с базы путешественник, если он способен унести запас продуктов на X дней, при этом, ему разрешается возобновлять запас на той же базе ровно Y раз и делать склады на маршруте.

Задача о пяти шапках.
комбинаторная задача
Пять мальчиков обменялись своими шапками так, что у каждого была надета чужая шапка. Сколькими способами можно обменяться?

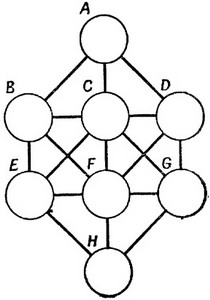
Задача о расстановке цифр.
числовая головоломка
Цифры от 1 до 8 надо расставить в восьми кружках фигуры, изображенной на рисунке, так, чтобы никакие два последовательных числа не стояли в кружках, соединенных друг с другом "напрямик". Например, если в самом верхнем кружке стоит цифра 5, то ни в один из трех кружков (В, С, D) следующего ряда уже нельзя вписать цифру 4 или 6, потому что каждый из этих кружков соединяется с верхним прямой линией.

Продолжение списка задач на букву "З"

◄ Назад 6 7 8 9 10 Вперёд ►