Задача о пауке и мухе.

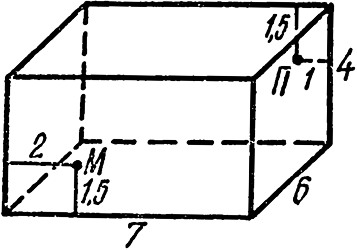
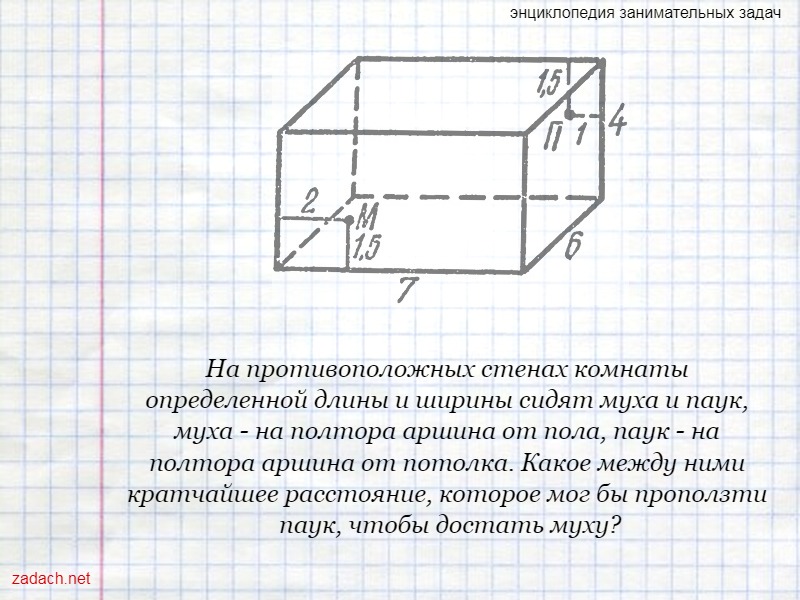
На противоположных стенах комнаты определенной длины и ширины сидят муха и паук, муха - на полтора аршина от пола, паук - на полтора аршина от потолка. Какое между ними кратчайшее расстояние, которое мог бы проползти паук, чтобы достать муху?

Ответ

10,77 аршина

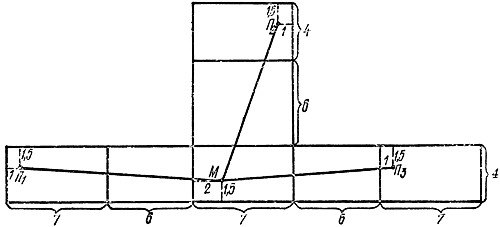
Решение задачи

Об этой задаче упоминается в дневнике секретаря Л. Н. Толстого В. Булгакова. Пусть длина комнаты 7 аршин, ширина - 6, высота - 4. Предположим, что муха сидит на большой стене на расстоянии двух аршин от угла, а паук - на противоположной стене - 4 на расстоянии одного аршина от ближайшего к нему угла. Эту задачу лучше всего решать графически. Сделаем развертку комнаты и соединим отрезками прямой точку, где сидит паук, с точкой, где сидит муха. Ясно, что решений будет три по числу различных разверток. Действительно, паук может ползти или только по стенам, или только по стенам и потолку, или по стенам и полу. Поскольку расстояния от мухи до пола и от паука до потолка одинаковы, то пути через пол и потолок равноценны. Следовательно, для этих двух путей и берется общая развертка, изображенная на рисунке. Пользуясь разверткой и применяя теорему Пифагора, получаем:

МП₁ = √197 = 14,04;
МП₂ = √116 = 10,77;
МП₃ = √145 = 12,04.

Следовательно, из трех возможных решений наименьшее будет 10,77 аршина, что и является ответом задачи.

О задаче

Категория: Старинные задачи, Геометрические задачи,
Степень сложности: сложная.
Ключевые слова: комната, муха, паук, пол, стена, Толстой Лев,
Источник: Сборник старинных задач по элементарной математике,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.