
|

|
Задачи с перестановками
![]()
Задачи с перестановками являются частью комбинаторики. Хорошей иллюстрацией данной категории могут послужить задачи про рукопожатия. В одной из них говорится: участники встречи обменялись рукопожатиями, и кто-то подсчитал, что всех рукопожатий было 66. Сколько человек явилось на встречу?
Список занимательных задач в категории "Задачи с перестановками"
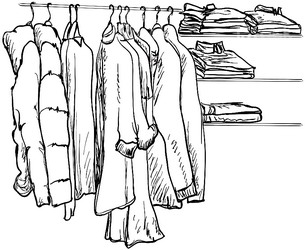
 3 пиджака 4 брюк и 5 жилетов.
3 пиджака 4 брюк и 5 жилетов.комбинаторная задача, задача с перестановками
Петров, имея 3 пиджака, 4 брюк и 5 жилетов, уверяет приятелей, что может более месяца (30 дней) ежедневно изменять свой костюм. Приятели не поверили, и у них состоялась сделка на следующих условиях: если Петров повторит костюм ранее месяца, то за каждый недостающий до месяца день он платит 10 рублей; если же он долее месяца будет ежедневно изменять свой костюм, то за первый день сверх месяца он получит 1 рубль, за второй - 2 рубля, за третий - 3 рубля и т. д. Выиграет или проиграет Петров и сколько?

 5 брюк 8 жилетов и 7 сюртуков.
5 брюк 8 жилетов и 7 сюртуков.комбинаторная задача, задача с перестановками
Мужчина имеет 5 брюк, 8 жилетов и 7 сюртуков. В скольких различных костюмах он может появляться?
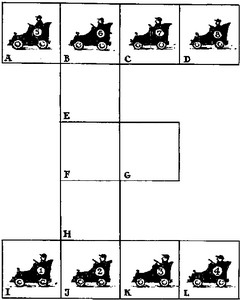
 Автомобильный гараж.
Автомобильный гараж.комбинаторная задача, задача с перестановками
На рисунке изображен план автомобильного гаража, содержащего 12 помещений для 12 автомобилей. В каждом помещении может стать только один автомобиль. Сейчас в гараже 8 машин: 4 машины обозначены цифрами 1, 2, 3, 4, стоят в помещениях I, J, K, L, а 4 машины, обозначенные цифрами 9, 10, 11, 12, стоят в помещениях A, B, C, D. Автомобили 1, 2, 3 и 4 необходимо поменять местами с автомобилями 5, 6, 7 и 8 за наименьшее число переездов. Примечание: выезжать за пределы гаражного комплекса автомобили не могут, два автомобиля двигаться одновременно не могут и в каждом отсеке гаража помещается только один автомобиль.

 Бесплатный обед.
Бесплатный обед.комбинаторная задача, задача с перестановками
Десять молодых людей решили отпраздновать окончание средней школы товарищеским обедом в ресторане. Когда все собрались, и первое блюдо было подано, заспорили о том, как усесться вокруг стола. Одни предлагали разместиться в алфавитном порядке, другие - по возрасту, третьи - по успеваемости, четвертые - по росту и т. д. Спор затянулся, суп успел остыть, а за стол никто не садился. Примирил всех официант, обратившийся к ним с такой речью:
- Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.
Все сели как попало. Официант продолжал:
- Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда - обещаю торжественно - я начну ежедневно угощать вас бесплатно самыми изысканными обедами. Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами. Однако, им не пришлось дождаться этого дня. Почему?
 В одной области 10 городов и каждые два города соединены шоссейной дорогой.
В одной области 10 городов и каждые два города соединены шоссейной дорогой.комбинаторная задача, задача с перестановками, задача на графы
В одной области 10 городов и каждые два города соединены шоссейной дорогой (каждый город соединен дорогой со всеми остальными городами). Сколько всего шоссейных дорог, соединяющих города этой области?

 В одной школе обучалось вдвое больше девочек, чем мальчиков.
В одной школе обучалось вдвое больше девочек, чем мальчиков.комбинаторная задача, задача с перестановками
В одной школе обучалось вдвое больше девочек, чем мальчиков. Заведующий ввел обычай: ежедневно поутру каждый мальчик должен был делать поклон заведующему, каждому из своих товарищей-мальчиков и каждой девочке, каждая девочка также должна была делать поклон заведующему, каждой своей подруге и каждому мальчику. Этот церемонный обычай строго соблюдался, и поэтому ежедневно утром можно было насчитать 900 поклонов. Сколько было в школе мальчиков и девочек?
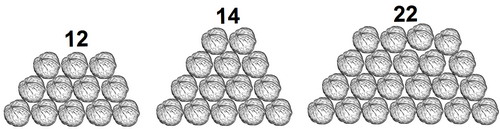
 В трех кучках 22 14 и 12 орехов.
В трех кучках 22 14 и 12 орехов.комбинаторная задача, задача с перестановками, решение задачи с конца
В трех кучках 22, 14 и 12 орехов. Требуется путем трех перекладываний уравнять число орехов в каждой кучке, соблюдая при этом условие: из одной кучки разрешается перекладывать в другую лишь столько орехов, сколько их имеется в этой второй кучке.

 Две шашки.
Две шашки.комбинаторная задача, задача с перестановками, задача на шахматной доске
На пустую шашечную доску надо поместить две шашки разного цвета. Сколько различных положений могут они занимать на доске?

 Девятьсот поклонов.
Девятьсот поклонов.комбинаторная задача, задача с перестановками
В одной школе обучалось вдвое больше девочек, чем мальчиков. Заведующий ввел обычай: ежедневно поутру каждый мальчик должен был делать поклон заведующему, каждому из своих товарищей-мальчиков и каждой девочке, каждая девочка также должна была делать поклон заведующему, каждой своей подруге и каждому мальчику. Этот церемонный обычай строго соблюдался, и поэтому ежедневно утром можно было насчитать 900 поклонов. Сколько было в школе мальчиков и девочек?

 Десять молодых людей решили отпраздновать окончание средней школы.
Десять молодых людей решили отпраздновать окончание средней школы.комбинаторная задача, задача с перестановками
Десять молодых людей решили отпраздновать окончание средней школы товарищеским обедом в ресторане. Когда все собрались, и первое блюдо было подано, заспорили о том, как усесться вокруг стола. Одни предлагали разместиться в алфавитном порядке, другие - по возрасту, третьи - по успеваемости, четвертые - по росту и т. д. Спор затянулся, суп успел остыть, а за стол никто не садился. Примирил всех официант, обратившийся к ним с такой речью:
- Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.
Все сели как попало. Официант продолжал:
- Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда - обещаю торжественно - я начну ежедневно угощать вас бесплатно самыми изысканными обедами. Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами. Однако, им не пришлось дождаться этого дня. Почему?
Продолжение списка задач:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
Задачи по географии |
Задачи по физике |
Задачи на движение |
Задачи на вероятность |
Задачи про возраст |
Задачи с часами |
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |
