Задача о прыгуне.

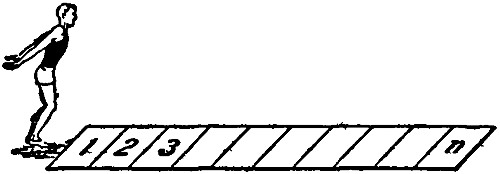
Сколькими, способами прыгун, стоящий перед клетками, начерченными на земле, может, достигнуть 10-й клетки, если он прыгает слева направо, приземляясь лишь в начерченных клетках, и длина его прыжков может быть произвольна?

Ответ

512

Решение задачи

Обозначим через u_s, число способов достижения s-й клетки. Для решения задачи следует учесть, что у прыгуна есть возможность (одна) прыгнуть на n-ю клетку, не приземляясь на промежуточных. Приземляться на k промежуточных клетках он может C^k_n-1 способами. Следовательно: u_n=1+C¹_n-1+C²_n-1+...+C^n-1_n-1=2^n-1. Таким образом, прыгун может достигнуть 10-й клетки 2⁹=512 способами.

О задаче

Категория: Комбинаторика, Задачи с перестановками,
Степень сложности: сложная.
Ключевые слова: 10, клетка, прыгун, спортсмен,
Источник: Математические игры и развлечения,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Сколько получится, если сложить вместе следующие числа: наибольшее однозначное, наибольшее двузначное, наибольшее трехзначное, наибольшее четырехзначное и наибольшее пятизначное?

a) 111105
b) 11110
c) 12345
d) 11111