≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Комбинаторика

Комбинаторика посвящена решению задач, связанных с выбором и расположением некоторого множества элементов в соответствии с определенными правилами. Простейшими примерами комбинаторных конфигураций являются задачи с перестановками. Одной из древнейших комбинаторных задач считается задача индийского математика Магавиры.

Список занимательных задач в категории "Комбинаторика"

137 человек записались для участия в соревнованиях по теннису
комбинаторная задача, задача с подвохом
137 человек записались для участия в соревнованиях по теннису, проводимых по олимпийской системе. Для игр первого круга все игроки должны разбиться на пары, но, поскольку 137 - нечетное число, одному игроку нехватает партнера и ему разрешается перейти в следующий круг без игры. Разбиение игроков на пары производится в каждом круге, и каждый раз один из игроков, оставшись без партнера, переводится в следующий круг. Сколько игр будет сыграно, прежде чем определится чемпион, если программа соревнований составлена с таким расчетом, чтобы свести число встреч до минимума?

3 пиджака 4 брюк и 5 жилетов.
комбинаторная задача, задача с перестановками
Петров, имея 3 пиджака, 4 брюк и 5 жилетов, уверяет приятелей, что может более месяца (30 дней) ежедневно изменять свой костюм. Приятели не поверили, и у них состоялась сделка на следующих условиях: если Петров повторит костюм ранее месяца, то за каждый недостающий до месяца день он платит 10 рублей; если же он долее месяца будет ежедневно изменять свой костюм, то за первый день сверх месяца он получит 1 рубль, за второй - 2 рубля, за третий - 3 рубля и т. д. Выиграет или проиграет Петров и сколько?

5 брюк 8 жилетов и 7 сюртуков.
комбинаторная задача, задача с перестановками
Мужчина имеет 5 брюк, 8 жилетов и 7 сюртуков. В скольких различных костюмах он может появляться?

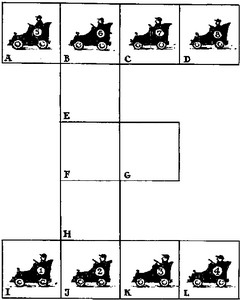
Автомобильный гараж.
комбинаторная задача, задача с перестановками
На рисунке изображен план автомобильного гаража, содержащего 12 помещений для 12 автомобилей. В каждом помещении может стать только один автомобиль. Сейчас в гараже 8 машин: 4 машины обозначены цифрами 1, 2, 3, 4, стоят в помещениях I, J, K, L, а 4 машины, обозначенные цифрами 9, 10, 11, 12, стоят в помещениях A, B, C, D. Автомобили 1, 2, 3 и 4 необходимо поменять местами с автомобилями 5, 6, 7 и 8 за наименьшее число переездов. Примечание: выезжать за пределы гаражного комплекса автомобили не могут, два автомобиля двигаться одновременно не могут и в каждом отсеке гаража помещается только один автомобиль.

Бесплатный обед.
комбинаторная задача, задача с перестановками
Десять молодых людей решили отпраздновать окончание средней школы товарищеским обедом в ресторане. Когда все собрались, и первое блюдо было подано, заспорили о том, как усесться вокруг стола. Одни предлагали разместиться в алфавитном порядке, другие - по возрасту, третьи - по успеваемости, четвертые - по росту и т. д. Спор затянулся, суп успел остыть, а за стол никто не садился. Примирил всех официант, обратившийся к ним с такой речью:
- Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.
Все сели как попало. Официант продолжал:
- Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда - обещаю торжественно - я начну ежедневно угощать вас бесплатно самыми изысканными обедами. Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами. Однако, им не пришлось дождаться этого дня. Почему?

Брошены два игральных кубика.
задача на вероятность, комбинаторная задача
Брошены два игральных кубика. Какая сумма очков на их верхних гранях наиболее вероятна?

Брошены три игральных кубика.
задача на вероятность, комбинаторная задача
Брошены три игральных кубика. Какова вероятность, что сумма очков на их верхних гранях будет равна их произведению?

В одной области 10 городов и каждые два города соединены шоссейной дорогой.
комбинаторная задача, задача с перестановками, задача на графы
В одной области 10 городов и каждые два города соединены шоссейной дорогой (каждый город соединен дорогой со всеми остальными городами). Сколько всего шоссейных дорог, соединяющих города этой области?

В одной школе обучалось вдвое больше девочек, чем мальчиков.
комбинаторная задача, задача с перестановками
В одной школе обучалось вдвое больше девочек, чем мальчиков. Заведующий ввел обычай: ежедневно поутру каждый мальчик должен был делать поклон заведующему, каждому из своих товарищей-мальчиков и каждой девочке, каждая девочка также должна была делать поклон заведующему, каждой своей подруге и каждому мальчику. Этот церемонный обычай строго соблюдался, и поэтому ежедневно утром можно было насчитать 900 поклонов. Сколько было в школе мальчиков и девочек?

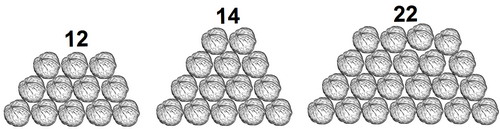
В трех кучках 22 14 и 12 орехов.
комбинаторная задача, задача с перестановками, решение задачи с конца
В трех кучках 22, 14 и 12 орехов. Требуется путем трех перекладываний уравнять число орехов в каждой кучке, соблюдая при этом условие: из одной кучки разрешается перекладывать в другую лишь столько орехов, сколько их имеется в этой второй кучке.

Продолжение списка задач:

1 2 3 4 5 Вперёд ►

◄ На предыдущую страницу