|
|
Графы
Граф - это математический объект, обладающий парными связями. Задачи на графы являются частью комбинаторики. Ярким примером задачи на графы может послужить задача Эйлера о семи кенигсбергских мостах.
Список занимательных задач в категории "Графы"
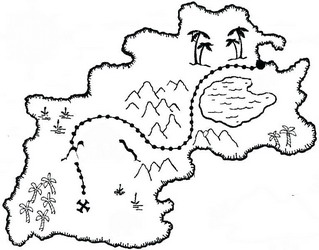
В одной области 10 городов и каждые два города соединены шоссейной дорогой.комбинаторная задача, задача с перестановками, задача на графы
В одной области 10 городов и каждые два города соединены шоссейной дорогой (каждый город соединен дорогой со всеми остальными городами). Сколько всего шоссейных дорог, соединяющих города этой области?
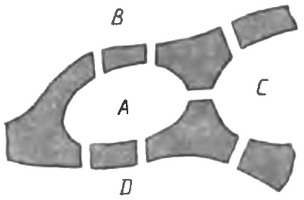
Задача о семи Кенигсбергских мостах.старинная задача, задача на графы
Леонард Эйлер в XVIII веке сформулировал задачу о семи мостах: на реке Преголя, в городе Кенигсберг (Калининград), имеется семь мостов. Возможно ли пройти по всем мостам, не вступая ни на один из них дважды?
Задачка про дорогу.комбинаторная задача, задача с перестановками, задача на графы
Человек, который живет в левом верхнем углу прямоугольника, состоящего из городских кварталов (см. рисунок), работает в конторе, находящейся в здании, занимающем правый нижний угол прямоугольника. Легко увидеть, что кратчайший путь, которым человек может добираться до работы, равен 10 кварталам. Но ему скучно ходить каждый день одной и той же дорогой, поэтому он пытается найти разные варианты кратчайшего маршрута. Сколько он сможет найти маршрутов, равных кратчайшему, соединяющих его дом с работой?
Лесная дача разделена просеками.комбинаторная задача, задача с перестановками, задача на графы
На рисунке изображен план лесной дачи, разделенной просеками на квадратные кварталы. Пунктирной линией обозначен путь по просекам от точки А до точки В. Это, конечно, не единственный путь между указанными точками по просекам. Сколько существует различных путей одинаковой длины?
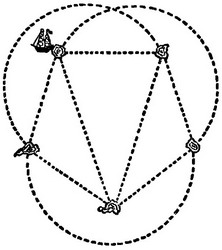
Пять островов.комбинаторная задача, задача с перестановками, задача на графы
На рисунке изображена карта с пятью островами. Каждый год корабль ходит по всем десяти указанным путям, но никогда в один и тот же год не ходит ни по одному пути дважды. Сколькими различными способами корабль сможет совершить эти десять ежегодных плаваний, отправляясь всегда от одного и того же острова и заканчивая плавание на том же острове, откуда впервые отчалил?
Рукопожатия и графы.задача на графы, задача на четность
Докажите, что число участников последнего конгресса биофизиков, обменявшихся рукопожатиями нечетное число раз, четно.
Семь мостов.старинная задача, задача на графы
Леонард Эйлер в XVIII веке сформулировал задачу о семи мостах: на реке Преголя, в городе Кенигсберг (Калининград), имеется семь мостов. Возможно ли пройти по всем мостам, не вступая ни на один из них дважды?
Число людей сделавших нечетное число рукопожатий четно.задача на графы, задача на четность
Докажите, что из всех людей, живших когда-либо на свете (и живущих сейчас), число людей, сделавших нечетное число рукопожатий, есть число четное.
Число путей.комбинаторная задача, задача с перестановками, задача на графы
На рисунке изображен план лесной дачи, разделенной просеками на квадратные кварталы. Пунктирной линией обозначен путь по просекам от точки А до точки В. Это, конечно, не единственный путь между указанными точками по просекам. Сколько существует различных путей одинаковой длины?
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Прогрессии |
 Комбинаторика |
 Задачи с перестановками |
 Графы |
 Принцип Дирихле |
 Множества |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |