|
|
Геометрические задачи
Продолжение списка занимательных задач в категории "Геометрические задачи" (страница 9)
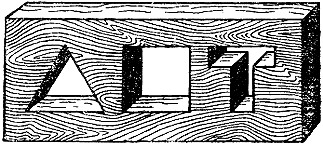
Дощечка с тремя отверстиями.геометрическая задача, задача на инвариант
Перед вами дощечка с тремя отверстиями. Может ли существовать одна пробка такой формы, чтобы закрывать все эти отверстия?
Дыни.геометрическая задача
Продаются две дыни. Одна - окружность 72 см - стоит 40 рублей. Другая - окружность 60 см - стоит 25 рублей. Какую дыню выгоднее купить?
Если бы возможно было вытянуть вещество всего земного шара в проволоку.геометрическая задача
Если бы возможно было вытянуть вещество всего земного шара в проволоку длиною от Земли (объем 1 триллион км3) до Солнца (расстояние 150 млн.км.), то какой толщины была бы эта проволока?
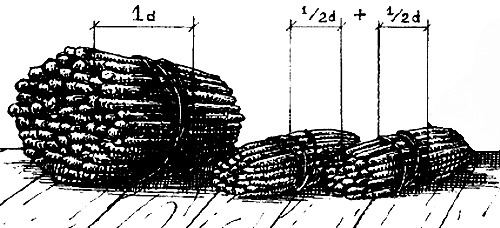
Женщина обыкновенно покупала у зеленщика спаржу.геометрическая задача
Одна женщина обыкновенно покупала у зеленщика спаржу большими пучками, каждый 40 см в окружности. Покупая, она мерила их, чтобы убедиться, что ее не обманывают. Но однажды у торговца не оказалось 40-сантиметрового пучка, и он предложил покупательнице за те же деньги два тонких пучка, каждый по 20 см в обхвате. Женщина обмерила пучки и, убедившись, что обхват каждого действительно равен 20 см, заплатила зеленщику столько же, сколько платила раньше за один толстый пучок. Она прогадала или выгадала на этой покупке?
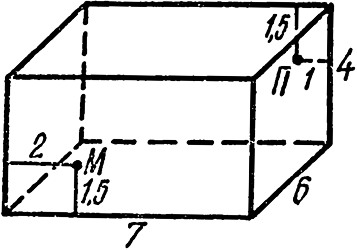
Жестянщик.задача на максимум и минимум, геометрическая задача
Жестянщик необходимо сделать прямоугольную цинковую цистерну с крышкой, которая должна вмещать ровно 1000 кубических футов воды. Необходимо определить размеры цистерны при которых на них пошло бы как можно меньше металла.
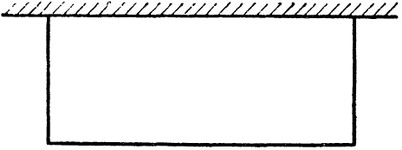
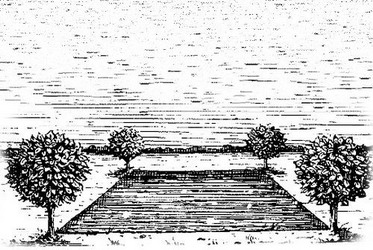
Заготовлен материал для постройки забора длиной 100 м.задача на максимум и минимум, геометрическая задача
Заготовлен материал для постройки забора длиной 100 м. Требуется огородить этим забором прямоугольный участок для детской площадки. Забор этот должен примыкать к стене дома. Как поставить этот забор так, чтобы площадь участка была наибольшей?
Задача Валлиса.старинная задача, геометрическая задача, задача на максимум и минимум
Показать алгебраически, что из прямоугольников одинакового периметра квадрат имеет наибольшую площадь.
Задача о пауке и мухе.старинная задача, геометрическая задача
На противоположных стенах комнаты определенной длины и ширины сидят муха и паук, муха - на полтора аршина от пола, паук - на полтора аршина от потолка. Какое между ними кратчайшее расстояние, которое мог бы проползти паук, чтобы достать муху?
Задача о пруде.геометрическая задача, задача на инвариант
Имеется квадратный пруд. По углам его, близ самой воды, растет 4 старых развесистых дуба. Пруд понадобилось расширить: сделать вдвое больше по площади, сохранив квадратную форму. Но вековые дубы трогать не хотят. Можно ли расширить пруд до требуемых размеров так, чтобы все 4 дуба, оставаясь на своих местах, оказались на берегах нового пруда?
Задача о сломанной палке.задача на вероятность, геометрическая задача
Палку случайным образом ломают на три части; какова вероятность того, что из обломков можно составить треугольник? (Точки перелома равномерно распределены по длине палки)
Продолжение списка задач:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Числовые головоломки |
 Числовые ребусы |
 Задачи на дроби |
 Задачи с процентами |
 Латинский квадрат |
 Магический квадрат |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |