Заготовлен материал для постройки забора длиной 100 м.

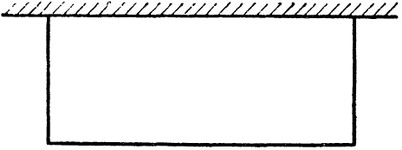
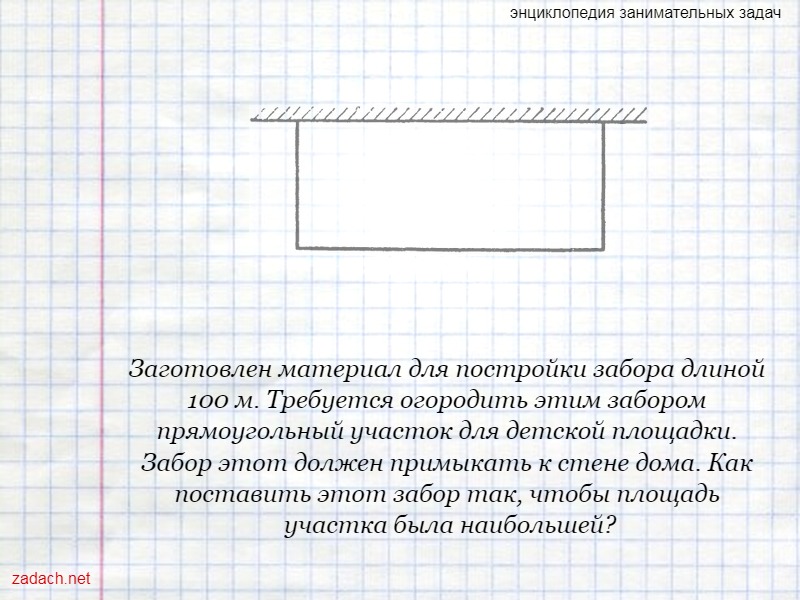
Заготовлен материал для постройки забора длиной 100 м. Требуется огородить этим забором прямоугольный участок для детской площадки. Забор этот должен примыкать к стене дома. Как поставить этот забор так, чтобы площадь участка была наибольшей?

Ответ

Длина участка 50 м, а ширина 25 м.

Решение задачи

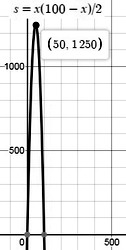
Обозначим длину участка через x, тогда его ширина будет (100-x)/2, а площадь, соответственно, будет равна s=x^100-x/₂=50x-^x²/₂. Остается определить, при каком значении x будет иметь наибольшее значение s. Для этого, например, можно построить график, как показано на рисунке. Теперь очевидно, что участок будет иметь наибольшую площадь при длине x=50 м, а ширине (100-50)/2=25 м.
Задача может быть решена не только графическим, но и алгебраическим способом: Рассмотрим общий случай. Одна сторона прямоугольника x, другая p-x, где p - полупериметр. Тогда площадь s=x(p-x) или x²-px+s=0, откуда x=_p/₂±√(^p²/₄-s). Очевидно, что для действительных значений x необходимо, чтобы ^p²/₄ было больше s, и наибольшее значение s=^p²/₄. Следовательно, x=^p/₂.

О задаче

Категория: Задачи на максимум и минимум, Геометрические задачи,
Степень сложности: средняя.
Ключевые слова: 100, дом, забор, изгородь, площадь, прямоугольник, стена, участок,
Источник: Математическая шкатулка,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Рассказывают, что в начальной школе, где учился Карл Гаусс (1777-1855), ставший потом знаменитым математиком, учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал детям задание - вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Попробуйте и вы быстро выполнить это задание.

a) 10000
b) 5050
c) 5000
d) 10100