|
|
Комбинаторика
Продолжение списка занимательных задач в категории "Комбинаторика" (страница 8)
Трое играли в шашки.логическая задача, комбинаторная задача, задача на шахматной доске
Трое играли в шашки. Всего сыграно 3 партии. Сколько партий сыграл каждый?
У одного человека было 7 друзей.комбинаторная задача
У одного человека было 7 друзей. Первый посещал его каждый вечер, второй - каждый второй вечер, третий - каждый третий вечер, четвертый - каждый четвертый вечер и т. д. до седьмого друга, который являлся каждый седьмой вечер. Часто ли случалось, что этого человека в один и тот же вечер навещали все семеро друзей?
Участники заседания обменялись рукопожатиями.комбинаторная задача, задача с перестановками
Участники заседания обменялись рукопожатиями, и кто-то подсчитал, что всех рукопожатий было 66. Сколько человек явилось на заседание?
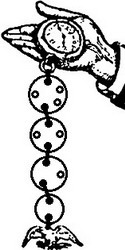
Цепочка для часов.комбинаторная задача, задача с перестановками
Цепочка для карманных часов составлена из четырех монет и брелока в виде фигурки орла. В монетах имелось соответственно пять, четыре, три и две дырки, так что монеты можно соединить между собой проволочками в большом числе комбинаций. Сколько различных цепочек, соединяющих часы с брелоком, можно сделать из пяти частей? Ни одно из размещений не должно повторять в точности никакое другое.
Четверо пассажиров.комбинаторная задача, задача с перестановками
Четверо пассажиров входят в вагон, в котором 6 свободных мест. Сколькими способами они могут разместиться?
Четыре льва.комбинаторная задача
Сколькими способами можно на доске 4 на 4 расположить четырех львов так, чтобы на любой горизонтали и вертикали находилось не более чем по одному льву? Отражения и повороты не считаются различными. Так, в приведенном на рисунке примере расположение львов вдоль второй диагонали мы не будем считать отличным от исходного.
Четыре школьника решили провести турнир в шашки.логическая задача, комбинаторная задача, задача на шахматной доске
Четыре школьника решили провести турнир в шашки. Чтобы выявить победителя, каждый должен сыграть со своими противниками по одной партии. Сколько всего партий должно быть сыграно в этом турнире?
Числа из одних и тех же цифр.комбинаторная задача, задача с перестановками
Сколько трехзначных чисел можно составить с помощью трех цифр 1, 2 и 3 так, чтобы одна и та же цифра встречалась в каждом числе не больше одного раза?
Число путей.комбинаторная задача, задача с перестановками, задача на графы
На рисунке изображен план лесной дачи, разделенной просеками на квадратные кварталы. Пунктирной линией обозначен путь по просекам от точки А до точки В. Это, конечно, не единственный путь между указанными точками по просекам. Сколько существует различных путей одинаковой длины?
Члены общества обменялись рукопожатиями.комбинаторная задача, задача с перестановками
Члены общества обменялись рукопожатиями, и всего вышло 210 рукопожатий. Сколько человек было в этом обществе?
Продолжение списка задач:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Прогрессии |
 Комбинаторика |
 Задачи с перестановками |
 Графы |
 Принцип Дирихле |
 Множества |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |