Цепочка для часов.

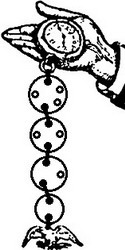
Цепочка для карманных часов составлена из четырех монет и брелока в виде фигурки орла. В монетах имелось соответственно пять, четыре, три и две дырки, так что монеты можно соединить между собой проволочками в большом числе комбинаций. Сколько различных цепочек, соединяющих часы с брелоком, можно сделать из пяти частей? Ни одно из размещений не должно повторять в точности никакое другое.

Ответ

92160

Решение задачи

Очевидно, что большую монету можно зацепить за любую из пяти дырок и повернуть (!) любой из двух сторон, что дает 5×2=10 комбинаций. Поскольку следующая монета может быть соединена восемью способами, то общее число комбинаций из двух первых монет равно 80. Если это умножить на 6 комбинаций следующей по размеру монеты, на 4 комбинации последней монеты и на 2 положения орла, то, располагая монеты по уменьшающимся размерам, мы получим 3840 комбинаций. Поскольку мы можем переставить между собой 4 монеты 4!=24 способами, то общее число всевозможных комбинаций равно 3840×24=92160.

О задаче

Категория: Комбинаторика, Задачи с перестановками,
Степень сложности: средняя.
Ключевые слова: 4, 5, брелок, монета, проволока, цепь, часы,
Источник: Самые знаменитые головоломки мира,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Брат и сестра пошли в лес за грибами. Брат нашел на 36 грибов больше, чем сестра. По дороге домой сестра попросила у брата несколько грибов, чтобы у них стало равное количество. Сколько грибов дал брат сестре?

a) 9 грибов
b) 18 грибов
c) 36 грибов
d) 27 грибов