≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Комбинаторика

Продолжение списка занимательных задач в категории "Комбинаторика" (страница 2)

В школе 5 кружков.
комбинаторная задача
В школе имеется 5 кружков: слесарный, столярный, фотографический, шахматный и хоровой. Слесарный кружок занимается через день, столярный - через 2 дня на 3-й, фотографический - каждый 4-й день, шахматный - каждый 5-й день и хоровой - каждый 6-й день. Первого января собрались в школе все 5 кружков, а затем занятия велись в назначенные по плану дни, без отступлений от расписания. Сколько в первом квартале было еще вечеров, когда собирались в школе все 5 кружков?

Восемь ладей.
задача на шахматной доске, комбинаторная задача
Сколькими различными способами 8 ладей можно расположить на шахматной доске так, чтобы при этом каждая клетка оказалась либо занятой, либо под угрозой нападения, но чтобы ни одна ладья не была защищена другой ладьей? Один из возможных способов, для примера, показан на рисунке.

Две ладьи.
задача на шахматной доске, комбинаторная задача
На шахматную доску надо поставить две ладьи так, чтобы они не были под боем друг друга. Сколько существует различных способов такой расстановки ладей? (Цвет ладей не учитывается.)

Две шашки.
комбинаторная задача, задача с перестановками, задача на шахматной доске
На пустую шашечную доску надо поместить две шашки разного цвета. Сколько различных положений могут они занимать на доске?

Девятьсот поклонов.
комбинаторная задача, задача с перестановками
В одной школе обучалось вдвое больше девочек, чем мальчиков. Заведующий ввел обычай: ежедневно поутру каждый мальчик должен был делать поклон заведующему, каждому из своих товарищей-мальчиков и каждой девочке, каждая девочка также должна была делать поклон заведующему, каждой своей подруге и каждому мальчику. Этот церемонный обычай строго соблюдался, и поэтому ежедневно утром можно было насчитать 900 поклонов. Сколько было в школе мальчиков и девочек?

Десять молодых людей решили отпраздновать окончание средней школы.
комбинаторная задача, задача с перестановками
Десять молодых людей решили отпраздновать окончание средней школы товарищеским обедом в ресторане. Когда все собрались, и первое блюдо было подано, заспорили о том, как усесться вокруг стола. Одни предлагали разместиться в алфавитном порядке, другие - по возрасту, третьи - по успеваемости, четвертые - по росту и т. д. Спор затянулся, суп успел остыть, а за стол никто не садился. Примирил всех официант, обратившийся к ним с такой речью:
- Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.
Все сели как попало. Официант продолжал:
- Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т. д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда - обещаю торжественно - я начну ежедневно угощать вас бесплатно самыми изысканными обедами. Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами. Однако, им не пришлось дождаться этого дня. Почему?

Железнодорожные билеты.
комбинаторная задача, задача с перестановками
Железнодорожный кассир продает билеты от данной станции до любой другой на той же дороге в обоих направлениях. Всего на данной дороге 25 станций. Сколько различных образцов билетов заготовлено железной дорогой для всех ее касс?

Задача Магавиры.
комбинаторная задача, задача с перестановками, старинная задача
Назовите число различных ожерелий, которые можно получить из бриллиантов, сапфиров, изумрудов, кораллов и жемчугов? Примечание: ожерелье может содержать от одного до пяти различных камней, идущих в указанной условием задачи последовательности.

Задача на восемь королев.
задача на шахматной доске, комбинаторная задача
Определить все способы размещения восьми королев на обыкновенной шахматной доске, состоящей из 64 клеток, таким образом, чтобы ни одна королева не могла быть взята другой, то есть расставить в 8 клетках шахматной доски столько же королев так, чтобы они не встречались попарно ни на одной линии, параллельной краям доски или одной из ее диагоналей.

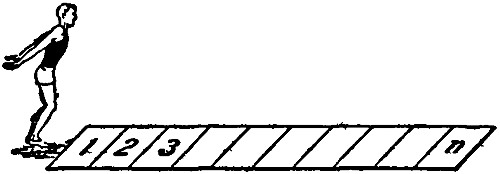
Задача о прыгуне.
комбинаторная задача, задача с перестановками
Сколькими, способами прыгун, стоящий перед клетками, начерченными на земле, может, достигнуть 10-й клетки, если он прыгает слева направо, приземляясь лишь в начерченных клетках, и длина его прыжков может быть произвольна?

Продолжение списка задач:

1 2 3 4 5 Вперёд ►

◄ На предыдущую страницу