
|

|
Геометрические задачи
![]()
Свойства основных геометрических фигур легли в основу занимательных задач по геометрии. При их решении пригодятся формулы для рассчета площади круга, треугольника и четырехугольника, объема шара и трапеции. Отдельные группы занимательных задач основаны на свойствах геометрически подобных фигур и теореме Пифагора. Несмотря на необходимость применения формул, задачи в данном разделе не лишены занимательности. К примеру, в одной из них, земной шар обвязали по экватору веревкой. Затем эту веревку удлинили на 1 метр и равномерно приподняли над экватором. Спрашивается, сможет ли в образовавшуюся между Землей и веревкой щель пролезть кошка?
Список занимательных задач в категории "Геометрические задачи"

 10 в 5 рядов по 4 в ряду.
10 в 5 рядов по 4 в ряду.геометрическая задача
Для изготовления праздничной иллюминации необходимо красиво разместить 10 лампочек в 5 рядов по 4 лампочки в каждом ряду. Как это сделать?
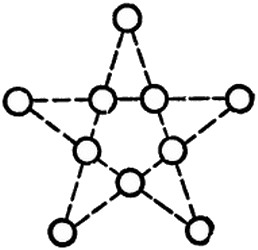
 10 монет в 5 рядов по 4 монеты в каждом.
10 монет в 5 рядов по 4 монеты в каждом.геометрическая задача
10 монет можно расположить в 5 рядов по 4 монеты в каждом ряду (ряд - прямая, проходящую через центры монет). Один вариант решения этой задачи представлен на рисунке. Придумайте другие варианты размещения.

 12 в 6 рядов по 4 в ряду.
12 в 6 рядов по 4 в ряду.геометрическая задача
Как расположить в праздничной иллюминации 12 лампочек в 6 рядов по 4 лампочки в каждом ряду?
 13 в 12 рядов по 3 в ряду.
13 в 12 рядов по 3 в ряду.геометрическая задача
Как рассадить 13 декоративных кустов в 12 рядов по 3 куста в каждом ряду?
 3 точки на сфере.
3 точки на сфере.геометрическая задача, задача на вероятность
На поверхности сферы наугад выбраны три точки. Чему равна вероятность того, что все три точки окажутся в одном полушарии?

 9 деревьев в 10 рядов по 3 дерева в каждом.
9 деревьев в 10 рядов по 3 дерева в каждом.старинная задача, геометрическая задача
Как посадить девять деревьев в десять рядов так, чтобы в каждом ряду было три дерева?

 9 точек 4 линии.
9 точек 4 линии.геометрическая задача
Как ломаной линией, состоящей из четырех отрезков, не отрывая карандаша от бумаги, перечеркнуть девять точек, расположенных так, как показано на рисунке?

 Аквариум.
Аквариум.геометрическая задача
У Володи был небольшой аквариум, который имел форму куба с ребром, равным 40 см. Вода в аквариуме была налита до уровня высотой в 18 см. Потом Володе купили новый аквариум, который имел форму прямоугольного параллелепипеда длиной в 48 см и шириной в 30 см. Володя перелил воду из старого в новый аквариум. Спрашивается, как высок стал уровень воды во втором аквариуме?

 Александровская колонна.
Александровская колонна.геометрическая задача
Александровская колонна в Санкт-Петербурге, состоящая из гранита, имеет в своей цилиндрической части 30 м. высоты и 4 м. в диаметре. Сколько весит эта гранитная колонна, если 1 см3 гранита весит 3 грамма.

 Бамбуковая трость высотой 10 футов надломлена.
Бамбуковая трость высотой 10 футов надломлена.старинная задача, геометрическая задача
Бамбуковая трость высотой 10 футов надломлена. Если пригнуть верхнюю часть к земле, то вершина трости будет отстоять от корня на 3 фута. Какой длины надломленная часть?
Продолжение списка задач:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
Задачи на внимательность |
Задачи с подвохом |
Эффект плюс-минус один |
Логические задачи |
Задачи со спичками |
Задачи с шестеренками |
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |
