|
|
Решение задачи с конца
Существует множество алгоритмов решения задачи. Один из них - решение задачи с конца.Его используют для вычисления каких-либо неизвестных данных на основе уже известного конечного результата. К примеру, подобный обратный расчет производится для решения известной задачи о продаже яблок:
Список занимательных задач в категории "Решение задачи с конца"
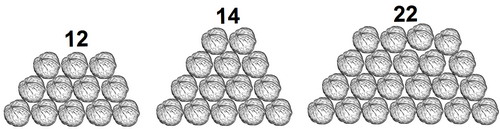
В трех кучках 22 14 и 12 орехов.комбинаторная задача, задача с перестановками, решение задачи с конца
В трех кучках 22, 14 и 12 орехов. Требуется путем трех перекладываний уравнять число орехов в каждой кучке, соблюдая при этом условие: из одной кучки разрешается перекладывать в другую лишь столько орехов, сколько их имеется в этой второй кучке.
В трех кучках лежит 24 спички.задача со спичками, решение задачи с конца
В трех кучках лежит 24 спички. Если из первой кучки положить во вторую столько, сколько находится во второй, затем из второй в третью столько, сколько в третьей, и, наконец, из третьей в первую столько, сколько оставалось в последней, то во всех кучках будет поровну. Сколько спичек в каждой кучке?
В ящике лежат лимоны.решение задачи с конца, задача на прогрессию
В ящике лежат лимоны. Сначала из него взяли половину всех лимонов и половину лимона, затем половину остатка и еще половину лимона, наконец, половину нового остатка и опять половину лимона. После этого в ящике остался 31 лимон. Сколько лимонов было в ящике вначале?
Веселый француз пришел в трактир с неизвестной суммой.старинная задача, решение задачи с конца
Веселый француз пришел в трактир с неизвестною суммою своего богатства, занял у содержателя столько денег, сколько у себя имел; из сей суммы издержал 1 рубль. С остатком пришел в другой трактир, где опять, занявши столько, сколько имел, издержал в оном также 1 рубль; потом пришел в третий и четвертый трактир, учинил то же, наконец, по выходе из четвертого трактира не имел ничего. Спрашивается количество его денег.
Веселый человек пришел в трактир с некоторой суммой денег.старинная задача, решение задачи с конца
Веселый француз пришел в трактир с неизвестною суммою своего богатства, занял у содержателя столько денег, сколько у себя имел; из сей суммы издержал 1 рубль. С остатком пришел в другой трактир, где опять, занявши столько, сколько имел, издержал в оном также 1 рубль; потом пришел в третий и четвертый трактир, учинил то же, наконец, по выходе из четвертого трактира не имел ничего. Спрашивается количество его денег.
Воришка с яблоками.решение задачи с конца, задача на прогрессию
Воришка залез в чужой сад и нарвал яблок. Незаметно подкрался сторож и схватил его, но сосчитав наворованные яблоки решил отпустить: - Ладно, - сказал сторож, - я отпущу тебя, только отдай мне половину всех яблок да еще пол-яблока. Ни у воришки ни у сторожа ножа не оказалось, но условие было выполнено. Через минуту воришка наткнулся на другого сторожа: - Отдай половину да еще пол-яблока, - сказал он. Воришка подчинился и снова стал убегать. У самого забора его остановил третий сторож. Он также отобрал половину всех яблок и еще пол-яблока. Уже за забором воришку схватил четвертый сторож: - Отдай половину да еще пол-яблока, - сказал он. Воришка обшарил все карманы, но нашел только одно яблоко. Пришлось и его отдать сторожу, а самому уйти не солоно хлебавши. Сколько яблок нарвал воришка в саду?
Восемь монет.решение задачи с конца, старинная задача
Трое имеют по некоторой сумме денег каждый. Первый дает из своих денег двум другим столько, сколько есть у каждого. После него второй дает двум другим столько, сколько каждый из них имеет. Наконец, и третий дает двум другим столько, сколько есть у каждого. После этого у всех троих оказывается по 8 экю (монет). Спрашивается, сколько денег было у каждого в начале?
Задача Кольриджа.старинная задача, решение задачи с конца
Некто забрел в сад, в котором имелось три калитки, у каждой из которых стоял сторож. Чтобы выйти из сада, необходимо было пройти через все калитки, не пропустив ни одной. Набрав некоторое количество яблок, он отдал половину всех яблок и еще пол-яблока человеку, стоявшему у первой калитки, половину того, что осталось, и еще пол-яблока - человеку, стоявшему у второй калитки, и половину всех оставшихся яблок и еще пол-яблока - человеку, стоявшему у третьей калитки. При этом, ни одно яблоко не разрезалось. Какое наименьшее число яблок удовлетворяет условиям задачи Кольриджа?
Имеется три неравные кучки спичек.задача со спичками, решение задачи с конца
Имеется три неравные кучки спичек. Во всех вместе 48 штук. Если из первой кучки переложить во вторую столько спичек, сколько в этой второй кучке имелось, затем из второй в третью переложить столько, сколько в этой третьей перед тем будет находиться, и, наконец, из третьей переложить в первую столько спичек, сколько в этой первой кучке будет тогда иметься, то число спичек во всех кучках станет одинаково. Сколько же было в каждой кучке первоначально?
Ипотека.задача с процентами, задача на прогрессию, решение задачи с конца
Один человек, желая приобрести некую собственность, но обладая лишь скромной суммой и питая отвращение ко всякого рода цифрам, закладам и процентам, заявил, что совершит покупку только в том случае, если будут приняты его условия. Согласно этим условиям, человек обязуется выплатить сразу 1000 долларов, а затем еще пять раз уплатить по 1000 долларов через каждые 12 месяцев. Эти выплаты должны были покрыть полную стоимость приобретения, включая проценты, набегавшие к моменту каждой выплаты. Сделка была заключена на этих условиях, а поскольку известно, что рассрочка дается из расчета 5% годовых, то спрашивается, чему равна собственная стоимость покупки?
Продолжение списка задач:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Геометрические задачи |
 Задачи на разрезание |
 Задачи на взвешивание |
 Задачи на переливание |
 Задачи о переправе |
 Шахматные задачи |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |