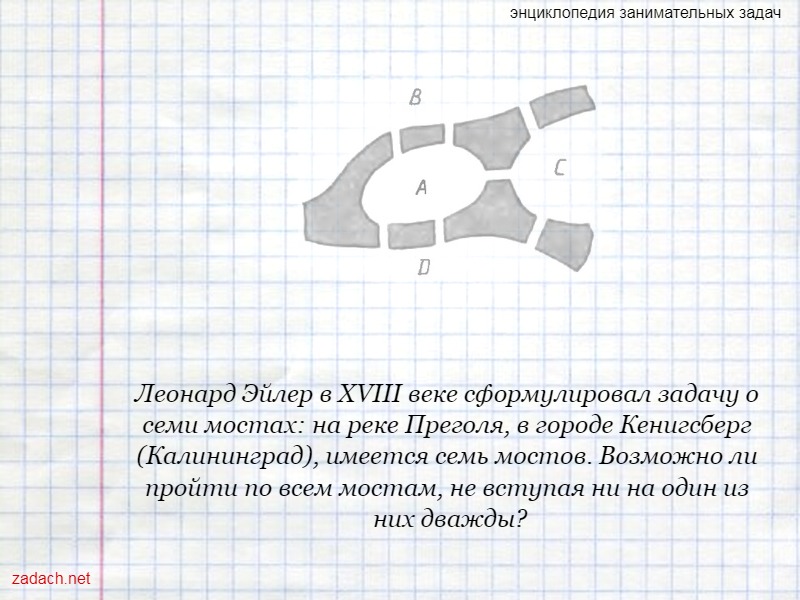
Задача о семи Кенигсбергских мостах.

Леонард Эйлер в XVIII веке сформулировал задачу о семи мостах: на реке Преголя, в городе Кенигсберг (Калининград), имеется семь мостов. Возможно ли пройти по всем мостам, не вступая ни на один из них дважды?

Ответ

Нет, невозможно.

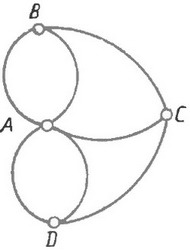
Решение задачи

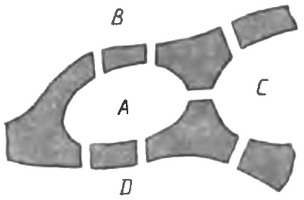
Если "сжать" острова в точки, как показано на рисунка, а мосты вытянуть в линии, то получим фигуру в виде геометрической сети. Решение задачи, в данном случае, сводится к вычеркиванию одним росчерком линии, состоящей из семи дуг, что невозможно, так как в каждой из четырех вершин A, B, C, D сходится число дуг, равное 3 или 5.
Иными словами, каково бы ни было расположение частей местности, всегда легко узнать, возможно или нет перейти все мосты по одному разу.
Задача неразрешима лишь в том случае, когда отдельных местностей с нечетными мостами больше двух.
Осуществима же она:
1) когда все местности обладают четным количеством мостов, причем начать обход можно откуда угодно;
2) когда местностей с нечетным числом мостов только две и когда обход начинается с одной из них и заканчивается на другой.

О задаче

Категория: Старинные задачи, Графы,
Степень сложности: сложная.
Ключевые слова: 7, Кенигсберг, мост, Эйлер Леонард,
Источник: Избранные математические развлечения, Старинные задачи, Старинные занимательные задачи, В царстве смекалки, Математические развлечения и игры, Математическая шкатулка, Веселое и занимательное о числах и фигурах, Математические эссе и развлечения, Математические игры и развлечения, Самые знаменитые головоломки мира, Математические развлечения с 55 фигурами, Сборник старинных задач по элементарной математике,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.