Пять островов.

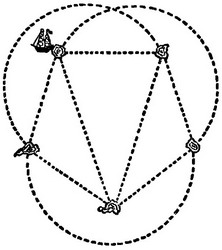
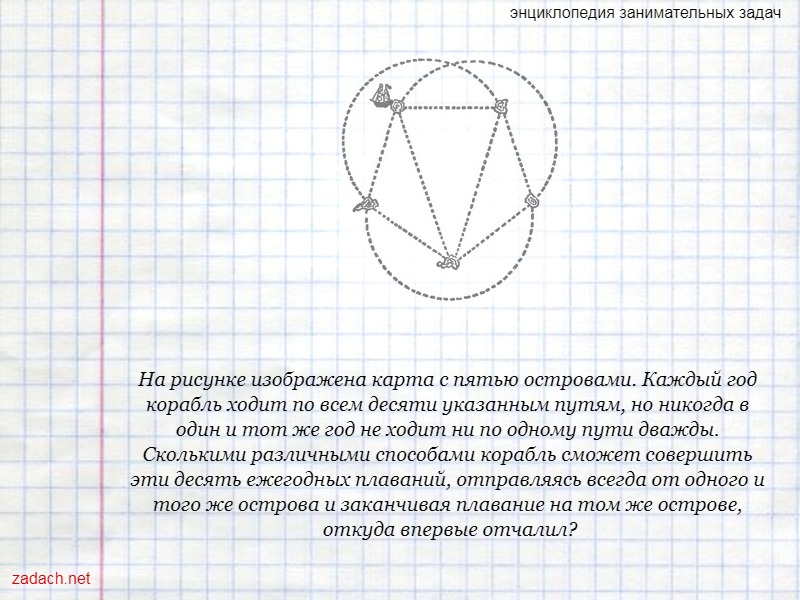
На рисунке изображена карта с пятью островами. Каждый год корабль ходит по всем десяти указанным путям, но никогда в один и тот же год не ходит ни по одному пути дважды. Сколькими различными способами корабль сможет совершить эти десять ежегодных плаваний, отправляясь всегда от одного и того же острова и заканчивая плавание на том же острове, откуда впервые отчалил?

Ответ

264

Решение задачи

Существует 264 различных способа, которыми корабль может совершить десять ежегодных плаваний, не проходя ни по какому пути дважды.

О задаче

Категория: Комбинаторика, Задачи с перестановками, Графы,
Степень сложности: средняя.
Ключевые слова: 5, 10, карта, корабль, остров, пароход, теплоход,
Источник: Кентерберийские головоломки,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Два приятеля отправились на несколько дней в лес. Каждый из них нес на палке через плечо узелок с провизией. Вес узелков и палок у приятелей одинаков. Кому палка меньше давит на плечо?

a) Мальчику справа.
b) Одинаково.
c) Мальчику слева.