|
|
Задачи с цифрой 2
Продолжение списка занимательных задач с цифрой 2 (страница 61)
Можно ли повернуть стол так, чтобы двое оказались против карточек с их именами?принцип Дирихле
Двадцать четыре участника важных переговоров проводят заседания за круглым столом, сидя на одинаковом расстоянии друг от друга. Место каждого участника за столом указано карточкой с его именем. Как-то раз после бурного обсуждения - одного из пунктов повестки дня в кулуарах участники переговоров, сев за стол, обнаружили, что по ошибке каждый из них занял не свое место. Точное расположение участников за столом не известно. Можно ли тем не менее повернуть стол так, чтобы по крайней мере двое из участников переговоров оказались против карточек с их именами?
Какие цифры скрыты на невидимых гранях кубиков?задача на внимательность
Переж вами оригинальный настольный календарь. Дату указывали цифры на передних гранях двух кубиков. На каждой грани кубика стоит по одной цифре от 0 до 9. Переставляя кубики, можно изобразить на календаре любую дату от 01, 02, 03, ... до 31. Какие цифры скрыты на невидимых гранях кубиков?
Урна содержит один шар про который известно что он либо белый либо черный.задача на вероятность
Урна содержит один шар, о котором известно, что он либо белый, либо черный. В урну кладут белый шар, после чего ее содержимое перемешивают и вытаскивают наудачу один шар, который оказывается белым. Какова после этого вероятность вытащить белый шар?
Современная задача Кэррола.задача на вероятность
В урне имеется несколько черных и несколько белых шаров. Точное число белых и черных шаров не известно, но по крайней мере по одному шару каждого цвета в урне есть. Шары извлекаются из урны по следующим правилам. Сначала из урны наудачу извлекается один шар и откладывается в сторону, затем наудачу извлекается второй шар. Если второй шар по цвету совпадает с первым, то его также откладывают в сторону и извлекают из урны третий шар. Вообще, если извлеченный из урны очередной шар того же цвета, что и предыдущий, то его откладывают в сторону. Если же извлеченный шар оказывается другого цвета, чем предыдущий, его снова кладут в урну и, тщательно перемешав ее содержимое, извлекают из урны следующий шар. Иначе говоря, извлеченный из урны шар откладывают в сторону лишь в том случае, если происходит "смена цвета". Оказывается, что независимо от начального соотношения между числом черных и белых шаров в урне существует фиксированная вероятность того, что последний извлеченный из урны шар будет черного цвета. Чему равна эта вероятность?
Ящик с носками.задача на вероятность
В ящике лежат красные и черные носки. Если из ящика наудачу вытягиваются два носка, то вероятность того, что оба они красные, равна 1/2. Каково минимальное возможное число носков в ящике?
Молчаливый союз.задача на вероятность, задача с подвохом
Двум незнакомым людям предлагается загадать произвольное натуральное число, причем если они оба называют одно и то же число, то получают премию. Какое бы число загадали вы?
Дилемма узника.логическая задача, задача на вероятность
Три узника, A, B и C, одинаково хорошего поведения ходатайствовали об освобождении на поруки. Администрация решила освободить двух из трех, что стало известно узникам, которые, однако, не знают, кто именно эти двое. У заключенного A в охране есть друг, который знает, кого отпустят на свободу, но A считает неэтичным осведомиться у охранника, будет ли он, A, освобожден. Все же A хочет спросить об имени одного узника, отличного от самого A, который будет отпущен на свободу. Прежде чем спрашивать, он оценивает вероятность своего освобождения как 2/3. A думает, что если охранник скажет , то его шансы уменьшатся до 1/2, так как в этом случае будут освобождены либо A и B, либо B и C. Однако A ошибается в своих расчетах. Объясните это.
Странное метро.задача на вероятность
Мэрвин кончает работу в случайное время между 15 и 17 часами. Его мать и его невеста живут в противоположных частях города. Мэрвин садится в первый подошедший к платформе поезд, идущий в любом направлении, и обедает с той из дам, к которой приедет. Мать Мэрвина жалуется на то, что он редко у нее бывает, но юноша утверждает, что его шансы обедать с ней и с невестой равны. Мэрвин обедал с матерью дважды в течение 20 рабочих дней. Объясните это явление.
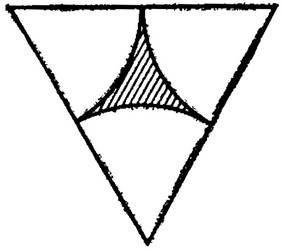
Мозаика.геометрическая задача
Пол готического собора выложен мозаикой, которая содержит приведенный на рисунке элемент, состоящий из трех равных дуг в равностороннем треугольнике со сторой 2 фута. Найдите площадь заштрихованной части.
Прошу, найдите отношенье наших лет.задача про возраст
Прошу, найдите отношенье наших лет
Но карандаш положен вам едва ли.
В два раза старше я, чем были вы в момент,
Когда я был такой, каким теперь вы стали.
Продолжение списка задач с цифрой 2:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Прогрессии |
 Комбинаторика |
 Задачи с перестановками |
 Графы |
 Принцип Дирихле |
 Множества |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |