|
|
Задачи с цифрой 2
Продолжение списка занимательных задач с цифрой 2 (страница 60)
Пинг и Понг.задача по географии, задача на внимательность
Жили-были два пингвина - Пинг и Понг. Они были очень дружны. Однажды Пинг забрался на высокий камень и долго грелся в лучах полярного солнца. Но вот Пинг заметил, что Понг с завистью смотрит на него, и тотчас уступил место приятелю. Как вы думаете, где на рисунке Пинг и где Понг?
Интересно, сколько мы весим с Бобиком?задача на взвешивание
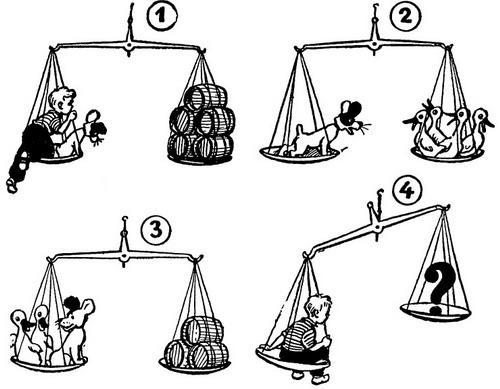
1. Интересно, сколько мы весим с Бобиком? Вместо гирь используем вот хотя бы эти пять пустых бочонков... Какое совпадение! Как по заказу - тютелька в тютельку!
2. А интересно: во сколько раз Бобик тяжелее утки? .. Ого, ровно в четыре раза!
3. Ну, а если к Бобику подсадить двух уток, то сколько бочонков понадобится, чтобы уравновесить их? М-да... Все-таки три бочонка.
4. Остается выяснить, сколько понадобится уток, чтобы уравновесить меня? Но на этот вопрос всякий догадливый человек ответит и не взвешивая нас!
Два герба справа от прямой, а две решетки слева.задача с подвохом, геометрическая задача
Проведите на листке бумаги вертикальную линию. Можно ли расположить на листке три монеты таким образом, чтобы два герба находились справа от прямой, а две решетки - слева?
Имеется два стальных бруска один из которых намагничен.задача по физике
Представьте себе, что вы заперты в комнате, где (так же как и на вас самих) нет ничего металлического, кроме двух совершенно одинаковых с виду железных брусков. Один из брусков намагничен. Необходимо установить, какой именно из двух брусков намагничен?
Две пластинки золота.задача с подвохом
Имеются пластинки золота одинаковой пробы двух размеров: 10- и 20-долларовые. Что дороже: килограмм 10-долларовых пластинок или полкилограмма 20-долларовых?
Задача про книжного червя.задача с подвохом
Первый том двухтомного издания толщиной в 2 см стоит на полке слева от второго тома толщиной в 21/2 см. В толщину каждого тома входит и толщина обложки. Обложки у обоих томов одинаковы и имеют толщину 1/8 см. Книжный червь прогрызает горизонтальную норку, начиная с первой страницы первого тома и финишируя на последней странице второго тома. Определите длину норки.
Среди жителей некоторой африканской деревни 800 женщин.занимательная задача
Среди жителей некоторой африканской деревни 800 женщин. Три процента из них носят по одной серьге, половина женщин, составляющих остальные 97%, носит по две серьги, а другая половина вообще не носит серег. Сколько серег можно насчитать в ушах у всего женского населения деревни?
Логик и два парикмахера.логическая задача
Логик, оказавшись случайно в небольшом городке и желая хоть как-то убить время, решил подстричься. В городке имеются лишь два мастера (у каждого из них своя парикмахерская). Заглянув к однс мастеру, логик увидел, что в салоне грязно, сам мастер одет неряшливо, плохо выбрит и небрежно подстрижен. В салоне другого мастера было идеально чисто, а владелец его был безукоризненно одет, чисто выбрит и акуратно подстрижен. Логик отправился стричься к первому парикмахеру. Почему?
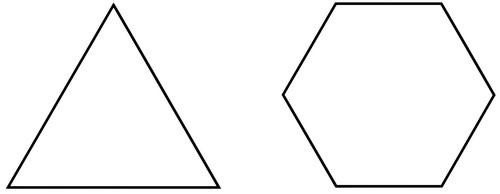
Равносторонний треугольник и правильный шестиугольник.геометрическая задача
Равносторонний треугольник и правильный шестиугольник имеют одинаковые периметры. Чему равна площадь шестиугольника, если площадь равностороннего треугольника равна 2?
Некая женщина либо всегда лжет, либо всегда говорит правду.логическая задача
Некая женщина либо всегда лжет, либо всегда говорит правду, либо всегда чередует правду и ложь. Как, задав ей два вопроса, которые требуют односложных ответов "да" и "нет", определить, какому из трех типов поведения она селедует?
Продолжение списка задач с цифрой 2:
◄ Назад 56 57 58 59 60 Вперёд ►
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Задачи по географии |
 Задачи по физике |
 Задачи на движение |
 Задачи на вероятность |
 Задачи про возраст |
 Задачи с часами |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |