≡
АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЭЮЯ#
§🔍

задача на максимум и минимум, геометрическая задача

Брус наибольшего объема.

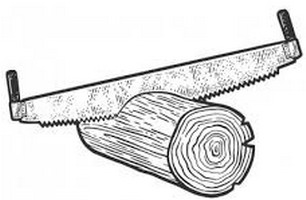
Из цилиндрического бревна надо выпилить прямоугольный брус наибольшего объема. Какой формы должно быть его сечение?

Ответ

Сечение бруса должно быть квадратным.

Решение задачи

Если стороны прямоугольного сечения х и y, то по теореме Пифагора x² + y² = d², где d - диаметр бревна. Объем бруса наибольший, когда площадь его сечения наибольшая, т. е. когда ху достигает наибольшей величины. Но если ху наибольшее, то наибольшим будет и произведение х²y². Так как сумма х² + y² неизменна, то, по доказанному ранее, произведение х²y² наибольшее, когда х² = y² или х = y. Таким образом, сечение бруса должно быть квадратным.

О задаче

• Категория: Задачи на максимум и минимум, Геометрические задачи,
• Степень сложности: средняя.
• Ключевые слова: бревно, брус, дерево, объем, прямоугольник, цилиндр,
• Источник: Занимательная алгебра,

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Имя: Почта:
Сообщение:

Проверочный код: 2+2×2=   

Спасибо. Ваше сообщение отослано Администратору.

Решите задачу

В колесе 10 спиц. Сколько промежутков между спицами?

a) 11
b) 10
c) 9

Занимательные задачи

Ещё больше занимательных задач собрано в следующих разделах:

Задачи по географии

Задачи по физике

Задачи на движение

Задачи на вероятность

Задачи про возраст

Задачи с часами