|
|
Геометрические задачи
Продолжение списка занимательных задач в категории "Геометрические задачи" (страница 29)
Пятью рядами.геометрическая задача
Десять шашек положите пятью рядами по четыре шашки в каждом.
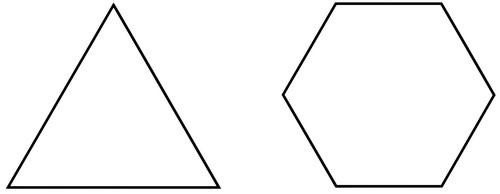
Равносторонний треугольник и правильный шестиугольник.геометрическая задача
Равносторонний треугольник и правильный шестиугольник имеют одинаковые периметры. Чему равна площадь шестиугольника, если площадь равностороннего треугольника равна 2?
Равноудаленные точки на сфере.геометрическая задача, задача на максимум и минимум
Чему равно наибольшее число точек, которые можно разместить на сфере так, чтобы расстояния между любыми двумя точками были равны?
Разделите число на две части чтобы произведение их было наибольшим.старинная задача, задача на максимум и минимум, числовая головоломка, геометрическая задача
Разделите данное число на такие две части, чтобы произведение их имело наибольшую величину.
Разместите 10 кружков на 5 отрезках.геометрическая задача
Как разместить 10 кружков на пяти равных отрезках так, чтобы на каждом из этих отрезков лежало по 4 кружка?
Разместите 6 кружков в 3 ряда по 3 кружка.геометрическая задача
Как разместить 6 кружков так, чтобы получилось 3 ряда по 3 кружка?
Разрушить периметры квадратов.комбинаторная задача, геометрическая задача
Сорок спичек расположены сеткой, как показано на рисунке. Какое наименьшее число спичек нужно убрать, чтобы периметр любого квадрата оказался разрушенным. Говоря о "любом" квадрате, мы имеем в виду не только 16 маленьких квадратов 1x2 но и 9 квадратов 2x2,4 квадрата 3x3 и большой квадрат 4x4 - внешний контур, то есть всего 30 квадратов.
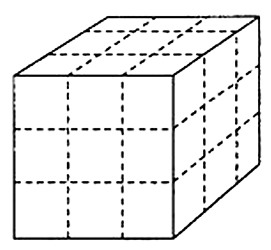
Распиливание куба.задача на разрезание, геометрическая задача
Один плотник решил распилить кубик размером 3×3×3 см на 27 кубиков с ребром в 1 см. Это делается очень просто: надо распилить куб по шести плоскостям, не разнимая его при этом на куски. Можно ли уменьшить число распилов, если после каждого из них складывать отпиленные части по-новому?
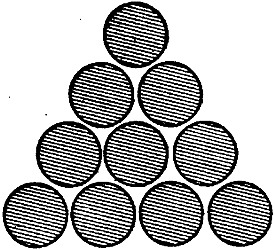
Расположите 10 монет треугольником.геометрическая задача
Расположите 10 монет треугольником, как показано на рисунке. Чему равно наименьшее число монет, которые необходимо изъять из треугольника, чтобы центры любых трех оставшихся монет не были расположены в вершинах равностороннего треугольника?
Расположите 4 шара чтоб каждый касался 3 других.геометрическая задача
Расположите 4 одинаковых шара так, чтобы каждый из них касался трех остальных.
Продолжение списка задач:
◄ Назад 26 27 28 29 30 Вперёд ►
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Числовые головоломки |
 Числовые ребусы |
 Задачи на дроби |
 Задачи с процентами |
 Латинский квадрат |
 Магический квадрат |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |