≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Задачи про сосуды

Продолжение списка занимательных задач про сосуды (страница 3)

В открытую бочку налита вода, на взгляд как будто до половины.
геометрическая задача
В открытую бочку налита вода, на взгляд как будто до половины. Но вы хотите знать точно, половина ли в ней налита, больше половины или меньше половины. У вас нет под рукой ни палки, ни вообще какого бы то ни было инструмента для обмера бочки. Каким образом могли бы вы убедиться, налита ли в бочке вода ровно до половины?

Некто отправился к источнику за водой с двумя кувшинами емкостью в 3 и 5 пинт.
задача на переливание, старинная задача
Некто отправился к источнику за водой с двумя кувшинами емкостью в 3 и 5 пинт. Как сможет он принести домой ровно 4 пинты воды?

Три хулигана отняли у одного гражданина сосуд, содержащий 24 унции бальзама.
задача на переливание, старинная задача
Три хулигана отняли у одного гражданина сосуд, содержащий 24 унции бальзама. Как ни торопились они скрыться, все же успели купить у продавца стеклянной посуды три флакона. Добравшись до безопасного места, они захотели разделить добычу на равные доли, но обнаружили, что купленные флаконы вмещают соответственно 5, 11 и 13 унций. Как же следует им поступить?

Головоломка трактирщика.
задача на переливание
В трактире стоит восьмипинтовый боченок эля (традиционный английский сорт пива), а также имеются две меры - одна в пять, а другая в три пинты величиной. Как трактирщику налить в каждую меру ровно по одной пинте? Разумеется, нельзя пользоваться никакими другими сосудами или приспособлениями.

Энергия растворенной пружины.
задача по физике
Стальную пружину согнули и поместили в сосуд. Затраченная работа превратилась в потенциальную энергию напряженной пружины. Затем, в сосуд наливают серную кислоту, и стальная пружина бесследно растворяется. Должник исчез: не с кого взыскать энергию, затраченную на сгибание пружины. Закон сохранения энергии как будто нарушен! Так ли?

Как разделить вино поровну между тремя братьями?
старинная задача, магический квадрат
В Кельне было три брата, имевших 9 сосудов с вином. Первый сосуд был емкостью в 1 кварту, второй содержал 2 кварты, и каждый следующий одной квартой больше, так что последний сосуд содержал уже 9 кварт. Требуется разделить вино поровну между тремя братьями, не смешивая содержимого сосудов.

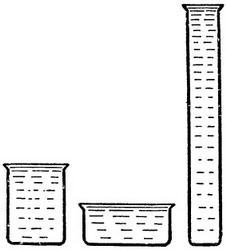
Три сосуда.
геометрическая задача
Три цилиндрических сосуда неодинаковых размеров. Средний вдвое ниже левого, зато в полтора раза шире его. Правый втрое выше левого, зато уже его вдвое. Который из этих сосуд самый вместительный?

Сколько воды в бочке?
геометрическая задача
Двое заспорили о содержимом бочки. Один спорщик говорил, что воды в бочке более, чем наполовину, а другой утверждал, что меньше. Как убедиться, кто прав, не употребляя ни палки, ни веревки, ни вообще какого-либо приспособления для измерения?

Задача про вино и воду.
логическая задача, задача по физике
В одной бутылке литр вина, в другой - литр воды. Из первой во вторую перелили ложечку вина, а затем из второй в первую отлили такую же ложечку полученной смеси. Чего теперь больше: воды в первой бутылке или вина во второй?

Задача про воду и спирт.
логическая задача, задача по физике
В одном стакане находилось m см³ воды, а в другом - n см³ спирта. Сначала из первого стакана перелили во второй а см³ воды, а затем (после тщательного перемешивания) обратно а см³ смеси. Считая для простоты, что объем смеси равен сумме объемов смешиваемых жидкостей, определить, чего будет больше примешано (по объему), спирта в первом стакане или воды - во втором?

Продолжение списка задач про сосуды:

1 2 3 4

◄ На предыдущую страницу