≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Задачи про плоскость

Список занимательных задач про плоскость

Три пчелы.
геометрическая задача
Три пчелы одновременно взлетели с полочки своего улья. Окажутся ли они снова в одной плоскости до того, как вернутся обратно в улей?

Трехногий стол.
геометрическая задача
Существует мнение, что стол о трех ногах никогда не качается, даже если ножки его и неравной длины. Верно ли это?

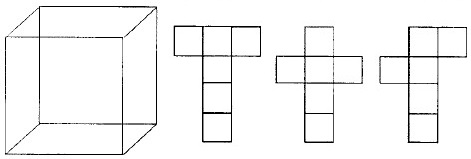
Сколькими способами можно развернуть куб на плоскости?
задача на разрезание, геометрическая задача
Если вы разрежете картонный куб вдоль ребер так, чтобы его можно было разогнуть и положить всеми 6-ю гранями на стол, то получите фигуру вроде трех, изображенных, для примера, на рисунке. Любопытно сосчитать: сколько различных фигур можно получить таким путем? Другими словами, сколькими способами можно развернуть куб на плоскости? Различными условимся считать две развертки, которые не совпадают при наложении друг с другом или одной из них с ее зеркальным отражением.

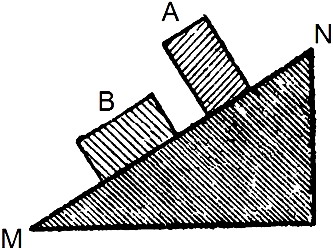
На наклонной плоскости.
задача по физике, задача на инвариант
Брусок в положении B скользит по наклонной плоскости, преодолевая трение. Можно ли быть уверенным, что он будет скользить и в положении А (если при этом не опрокидывается)?

Как разрезать куб чтобы получить шестиугольник?
задача на разрезание, геометрическая задача
Как разрезать куб на две равные части так, чтобы плоскость разреза представляла собой правильный шестиугольник?

Три ласточки.
геометрическая задача
Из одной точки вылетели 3 ласточки. Когда они будут в одной плоскости?

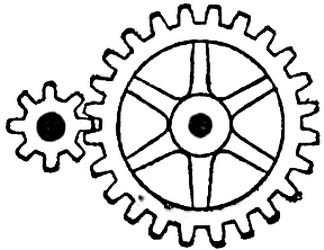
Будут ли вращаться колеса?
задача с шестеренками, задача на четность
В плоскости расположено несколько зубчатых колес так, что первое колесо сцеплено со вторым, второе - с третьим, третье - с четвертым и т. д. Последнее же колесо сцеплено с первым. Будут ли вращаться колеса такой системы?

Можно ли пересечь куб плоскостью так чтобы в сечении получился правильный треугольник?
задача на разрезание, геометрическая задача, задача на инвариант
Можно ли пересечь куб плоскостью так, чтобы в сечении получился равносторонний треугольник?

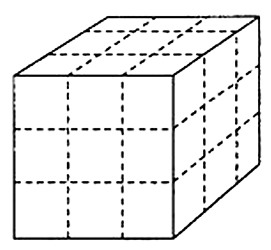
Распиливание куба.
задача на разрезание, геометрическая задача
Один плотник решил распилить кубик размером 3×3×3 см на 27 кубиков с ребром в 1 см. Это делается очень просто: надо распилить куб по шести плоскостям, не разнимая его при этом на куски. Можно ли уменьшить число распилов, если после каждого из них складывать отпиленные части по-новому?

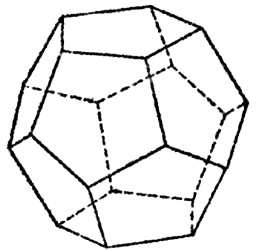
Неустойчивый многогранник.
геометрическая задача, задача по физике
Правильный выпуклый многогранник можно поставить на горизонтальную плоскость любой гранью. Поскольку центр тяжести правильного многоугольника совпадает с его центром, положение его будет устойчиво, на какую бы грань его ни поставили. Можно ли построить модель неправильного многогранника, который будет неустойчив, на какую бы грань его ни поставили?

◄ На предыдущую страницу