Будут ли вращаться колеса?

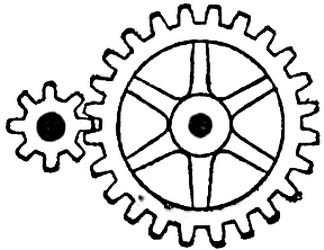
В плоскости расположено несколько зубчатых колес так, что первое колесо сцеплено со вторым, второе - с третьим, третье - с четвертым и т. д. Последнее же колесо сцеплено с первым. Будут ли вращаться колеса такой системы?

Ответ

Зависит от числа зубчатых колес.

Решение задачи

Если из двух сцепленных зубчатых колес одно вращается по часовой стрелке, то другое будет вращаться в направлении, противоположном вращению часовой стрелки. Поэтому, если пронумеровать последовательно сцепленные между собой зубчатые колеса, то все зубчатые колеса, имеющие нечетный номер, будут вращаться в одном и том же направлении, а имеющие четный номер - в противоположном. Если в системе из N зубчатых колес последнее, N-е колесо, будет сцеплено с первым, то это колесо может рассматриваться и как колесо 1-е и как колесо с номэром N+1. Если число N+1 окажется нечетным числом, т. е число N - четным числом, то система будет работать; если же N будет нечетным числом, то возникнет положение, при котором 1-е колесо должно будет одновременно вращаться в двух противоположных направлениях, что невозможно. Итак, система будет работать, если число N, четное.

О задаче

Категория: Задачи с шестеренками, Четность,
Степень сложности: средняя.
Ключевые слова: вращение, зубец, колесо, плоскость, шестеренка,
Источник: Сборник задач по математике на сообразительность,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Секретарь отпечатала четыре письма четырем разным людям и надписала четыре конверта. Предположим, что она вкладывает письма в конверты наугад. Какова вероятность того, что ровно три письма окажутся вложенными в конверты с адресами тех лиц, кому они предназначены?

a) 75%
b) 25%
c) 0%
d) 100%