|
|
Задачи про площадь
Продолжение списка занимательных задач про площадь (страница 2)
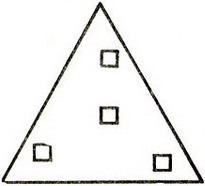
Участок с четырьмя колодцами.задача на разрезание
Участок с четырьмя колодцами (на рисунке обозначены квадратами), имеющий форму равностороннего треугольника, надо разделить на такие участки, чтобы они были одинаковы по форме, равны по площади и чтобы на каждом из них было по колодцу. Как это сделать?
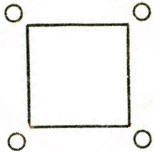
По углам бассейна квадратной формы стоят 4 столба.геометрическая задача, задача на инвариант
По углам бассейна квадратной формы стоят 4 столба. Потребовалось расширить этот бассейн так, чтобы площадь его стала в два раза больше, а форма осталась бы квадратной. Можно ли это сделать, не убирая столбов? Если можно, то как?
Как имея 22 спички сложить контур прямоугольника с наибольшей площадью?геометрическая задача, задача на максимум и минимум, задача со спичками
Как, имея 22 спички, сложить контур прямоугольника с наибольшей площадью? Ломать спички нельзя.
Стороны прямоугольника выражаются целыми числами.геометрическая задача
Стороны прямоугольника выражаются целыми числами. Какой длины должны они быть, чтобы периметр прямоугольника численно равнялся его площади?
На площади установлено 5 громкоговорителей.задача по физике, задача на максимум и минимум
На площади установлено 5 громкоговорителей, разбитых на две группы: в одной 2, в другой 3 аппарата. Расстояние между группами 50 м. Где надо стать, чтобы звуки обеих групп доносились с одинаковой силой?
Какой формы должен быть прямоугольный участок данной площади?задача на максимум и минимум, геометрическая задача
Какой формы должен быть прямоугольный участок данной площади, чтобы длина ограничивающей его изгороди была наименьшей?
Какой формы должен быть прямоугольный участок?задача на максимум и минимум, геометрическая задача
Какой формы должен быть прямоугольный участок, чтобы при данной длине изгороди площадь его была наибольшей?
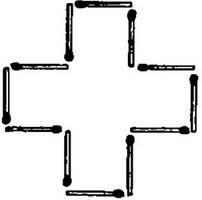
Крест из 12 спичекгеометрическая задача, задача со спичками
Из 12 спичек можно составить фигуру креста, изображенную на рисунке, площадь которого равна 5 "спичечным" квадратам. Измените расположение спичек так, чтобы контур фигуры охватывал площадь, равную только 4 "спичечным" квадратам. Пользоваться при этом услугами измерительных приборов нельзя.
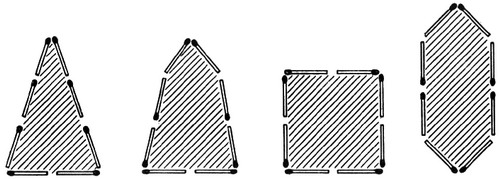
Как из 8 спичек сложить фигуру наибольшей площади?задача на максимум и минимум, геометрическая задача, задача со спичками
Из 8 спичек можно составить довольно разнообразные замкнутые фигуры. Некоторые из них представлены на рис. 70; площади их, конечно, различны. Задача состоит в том, чтобы составить из 8 спичек фигуру, охватывающую наибольшую площадь.
Основание Карфагена.геометрическая задача
Об основании древнего города Карфагена существует следующее предание. Дидона, дочь тирского царя, потеряв мужа, убитого рукой ее брата, бежала в Африку и высадилась со многими жителями Тира на ее северном берегу. Здесь она купила у нумидийского царя столько земли, "сколько занимает воловья шкура". Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, к которой впоследствии был пристроен город. Попробуйте вычислить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что воловья шкура имеет поверхность 4 м2, а ширину ремешков, на которые Дидона ее разрезала, принять равной 1 мм.
Продолжение списка задач про площадь:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Геометрические задачи |
 Задачи на разрезание |
 Задачи на взвешивание |
 Задачи на переливание |
 Задачи о переправе |
 Шахматные задачи |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |