|
|
Магический квадрат
Магический квадрат представляет собой таблицу, заполненную различными числами, при этом, их сумма в каждой строке, столбце и на обеих диагоналях - равны. Магический квадрат был известен еще 2200 лет до нашей эры, в Древнем Китае. Существует ряд занимательных задач, использующий свойства магического квадрата. В одной из них, необходимо разрезать циферблат часов на 6 частей так, чтобы во всех частях сумма чисел была одинакова.
Список занимательных задач в категории "Магический квадрат"
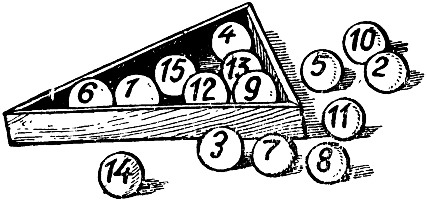
Биллиард.магический квадрат
Биллиардные шары перед началом игры укладываются в пирамиду в виде треугольника. Обычно их размещают в любом порядке. Попробуйте переставить шары в пирамиде таким образом, чтобы в каждом ряду, ограничивающем линию пирамиды, при сложении цифр очков каждого шара (от 1 до 15) получилось одинаковое число.
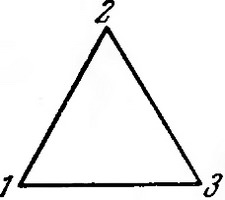
В вершинах треугольника записаны числа 1 2 3.магический квадрат
В вершинах треугольника числа 1, 2 и 3. Необходимо разместить числа 4, 5, 6, 7, 8, 9 по сторонам треугольника так, чтобы сумма всех чисел вдоль каждой стороны треугольника равнялась 17.
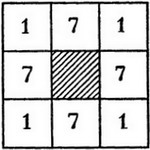
Винный шкаф.магический квадрат
У помещика в погребе был шкаф, похожий по форме на квадрат, разделенный на 9 ящиков (клеток). В среднем ящике была сложена пустая посуда, а в остальных были расставлены 32 бутылки вина так, что в каждом угловом ящике было по одной бутылке, а в каждом среднем ящике по семь бутылок. Словом, на каждой стороне квадрата было по 9 бутылок. Лакей помещика заметил, что скупой хозяин, проверяя число бутылок, считает только бутылки по сторонам квадрата. Для помещика важно лишь, чтобы на каждой стороне квадрата было по 9 бутылок. На следующий день лакей унес 4 бутылки, а остальные расставил так, чтобы на каждой стороне квадрата шкафа получилось по 9 бутылок. Помещик вскоре пересчитал бутылки по-своему и не догадался, что четыре из них украдены. Лакей был рад этому и на следующей неделе снова унес 4 бутылки, а остальные расставил так, что на каждой стороне шкафа было опять по 9 бутылок. Помещик и тут не заметил пропажи. Тогда лакей и в3 раз украл 4 бутылки, а остальные расставил так, что на каждой стороне квадратного шкафа по-прежнему оставалось по 9 бутылок. Как лакей расставлял бутылки после каждой кражи?
Волшебный треугольник.магический квадрат
В вершинах треугольника числа 1, 2 и 3. Необходимо разместить числа 4, 5, 6, 7, 8, 9 по сторонам треугольника так, чтобы сумма всех чисел вдоль каждой стороны треугольника равнялась 17.
Двумя прямыми линиями разделите циферблат на три части.задача с часами, магический квадрат
Как разделить циферблат часов двумя прямыми линиями на 3 части так, чтобы во всех частях сумма чисел была одинакова?
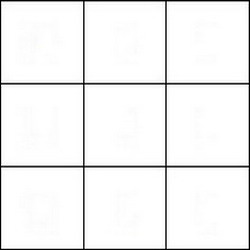
Задача Ло Шу.магический квадрат, старинная задача
Заполните натуральными числами от 1 до 9 квадратную таблицу 3 на 3 так, чтобы сумма чисел по всем строкам, столбцам и диагоналям равнялась одному и тому же числу - 15.
Как нужно разрезать циферблат часов на 6 частейзадача с часами, магический квадрат
Как нужно разрезать циферблат часов на 6 частей так, чтобы во всех частях сумма чисел была одинакова?
Как разделить вино поровну между тремя братьями?старинная задача, магический квадрат
В Кельне было три брата, имевших 9 сосудов с вином. Первый сосуд был емкостью в 1 кварту, второй содержал 2 кварты, и каждый следующий одной квартой больше, так что последний сосуд содержал уже 9 кварт. Требуется разделить вино поровну между тремя братьями, не смешивая содержимого сосудов.
Как разделить циферблат часов на 2 части?задача с часами, магический квадрат
Как разделить циферблат часов одной прямой линией на две части так, чтобы в каждой части сумма цифр была одинакова.
Как разделить циферблат часов на 3 части?задача с часами, магический квадрат
Как разделить циферблат часов двумя прямыми линиями на 3 части так, чтобы во всех частях сумма чисел была одинакова?
Продолжение списка задач:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Задачи по географии |
 Задачи по физике |
 Задачи на движение |
 Задачи на вероятность |
 Задачи про возраст |
 Задачи с часами |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |