Три монеты.

Три монеты лежат на столе, касаясь друг друга, а их центры образуют прямоугольный треугольник. Приведите их размеры, выражаемые наименьшими возможными целыми числами.

Ответ

Радиусы монет равны 1, 2 и 3.

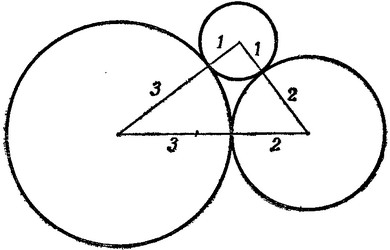
Решение задачи

Обозначим монеты в порядке возростания из радиусов как x, y, z, Тогда, по теореме Пифагора:
(x+y)² + (x+z)² = (y+z)²
Откуда: x² + 2xy + y² + x² + 2xz + z² - y² - 2yz - z² = 0, 2x² + 2xy + 2xz - 2yz = 0, 2x² + 2xy + 2xz = 2yz, x² + xy + xz = yz, x² + xy = z(y - x), z = (x² + xy) / (y - x). Таким образом,
z = ^{x(x + y)}/_{(y - x)}
Поскольку x - целое число больше 0, а в знаменателе не может быть 0, предположим, что x=1, y=x+1=2, тогда z=1(1+2)÷(2-1)=3. Таким образом, радиусы монет составляют 1, 2 и 3.
Найдем еще одну возможную комбинацию размеров монет: x=2, y=4, z=2(2+4)÷(4-2)=6

О задаче

Категория: Геометрические задачи,
Степень сложности: средняя.
Ключевые слова: 3, монета, стол, треугольник, центр, число,
Источник: Россыпи головоломок,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.