|
|
Задачи на вероятность
Продолжение списка занимательных задач в категории "Задачи на вероятность" (страница 5)
Секретарь отпечатала четыре письма четырем разным людям.задача на вероятность, задача с подвохом, задача на четность
Секретарь отпечатала четыре письма четырем разным людям и надписала четыре конверта. Предположим, что она вкладывает письма в конверты наугад. Какова вероятность того, что ровно три письма окажутся вложенными в конверты с адресами тех лиц, кому они предназначены?
Сколько раз надо бросать кубик до появления 6?задача на вероятность
Сколько в среднем раз надо бросать кость до появления шестерки?
Современная задача Кэррола.задача на вероятность
В урне имеется несколько черных и несколько белых шаров. Точное число белых и черных шаров не известно, но по крайней мере по одному шару каждого цвета в урне есть. Шары извлекаются из урны по следующим правилам. Сначала из урны наудачу извлекается один шар и откладывается в сторону, затем наудачу извлекается второй шар. Если второй шар по цвету совпадает с первым, то его также откладывают в сторону и извлекают из урны третий шар. Вообще, если извлеченный из урны очередной шар того же цвета, что и предыдущий, то его откладывают в сторону. Если же извлеченный шар оказывается другого цвета, чем предыдущий, его снова кладут в урну и, тщательно перемешав ее содержимое, извлекают из урны следующий шар. Иначе говоря, извлеченный из урны шар откладывают в сторону лишь в том случае, если происходит "смена цвета". Оказывается, что независимо от начального соотношения между числом черных и белых шаров в урне существует фиксированная вероятность того, что последний извлеченный из урны шар будет черного цвета. Чему равна эта вероятность?
Странное метро.задача на вероятность
Мэрвин кончает работу в случайное время между 15 и 17 часами. Его мать и его невеста живут в противоположных частях города. Мэрвин садится в первый подошедший к платформе поезд, идущий в любом направлении, и обедает с той из дам, к которой приедет. Мать Мэрвина жалуется на то, что он редко у нее бывает, но юноша утверждает, что его шансы обедать с ней и с невестой равны. Мэрвин обедал с матерью дважды в течение 20 рабочих дней. Объясните это явление.
Страстный игрок в кости.задача на вероятность, старинная задача
Страстный игрок в кости рыцарь де Мерэ хотел разбогатеть при помощи игры по особым правилам. Игральная кость бросалась 4 раза. Рыцарь бился об заклад, что при этом хотя бы один раз выпадет 6 очков. Какова вероятность выигрыша для рыцаря?
Суеверный велосипедистзадача на вероятность
До недавнего времени каждому велосипеду присваивался номер подобно тому, как это делается для автомашин. Эти номера были шестизначные. Некто купил себе велосипед, желая выучиться ездить на нем. Владелец велосипеда оказался на редкость суеверным человеком. Узнав о существовании повреждения велосипеда, именуемого "восьмеркой", он решил, что удачи ему не будет, если ему достанется велосипедный номер, в котором будет хоть одна цифра 8. Однако, идя за получением номера, он утешал себя следующим рассуждением. В написании каждого числа могут участвовать 10 цифр: 0, 1, ... , 9. Из них "несчастливой" является только цифра 8. Поэтому имеется лишь один шанс из десяти за то, что номер окажется "несчастливым". Правильно ли было это рассуждение?
Трамваи двух цветов.задача на вероятность
По улице, на которой я живу, курсируют трамваи двух цветов: желтого и красного. И тех и других одинаковое количество, и те и другие ходят с промежутками в десять минут. Ежедневно я совершаю несколько поездок в самые различные часы дня. Число поездок в вагонах каждого цвета должно составлять, очевидно, 50% общего чиста поездок: ведь, казалось бы, шансы попасть в желтый или красный трамвай одинаковы. Однако, ведя в течение нескольких месяцев записи, я заметил, что приблизительно 90% всех поездок были совершены в желтых трамваях и лишь 10% - в красных. Как это явление может быть объяснено арифметически?
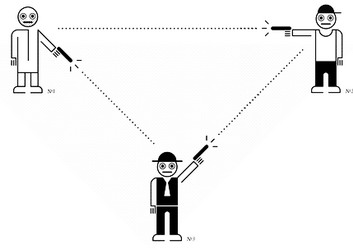
Трехсторонняя дуэль.логическая задача, задача на вероятность
Смит, Браун и Джонс, решив внести в обычную дуэль на пистолетах некоторое разнообразие, условились провести поединок по несколько измененным правилам. Вытащив жребий и узнав, кому из них выпало стрелять первым, кому - вторым и кому - третьим, они разошлись по своим местам, встав в вершинах равностороннего треугольника. Договорились, что каждый по очереди производит лишь один выстрел и может целиться в кого угодно. Дуэль продолжается до тех пор, пока не будут убиты любые два ее участника. Очередность стрельбы определяется только результатами жеребьевки и остается неизменной в течение всего поединка. Все три участника знают, что Смит никогда не промахивается, Браун попадает в цель в 80 % случаев, а Джонс, стреляющий хуже всех, промахивается так же часто, как и попадает в цель. Кто из дуэлянтов имеет более высокий шанс уцелеть, если считать, что все трое придерживаются оптимальных стратегий?
Урна содержит один шар про который известно что он либо белый либо черный.задача на вероятность
Урна содержит один шар, о котором известно, что он либо белый, либо черный. В урну кладут белый шар, после чего ее содержимое перемешивают и вытаскивают наудачу один шар, который оказывается белым. Какова после этого вероятность вытащить белый шар?
Хозяйка сварила 5 яиц.задача на вероятность
Хозяйка сварила 5 яиц: два вкрутую и три всмятку. Но она забыла отметить, какие именно яйца сварены вкрутую и какие всмятку, и подала их к столу на одном блюде. Вы наудачу берете с блюда два яйца. Стоит ли биться о заклад, ставя один рубль против пяти, что вам попадутся оба крутых яйца?
Продолжение списка задач:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Геометрические задачи |
 Задачи на разрезание |
 Задачи на взвешивание |
 Задачи на переливание |
 Задачи о переправе |
 Шахматные задачи |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |