В одной семье было много детей.

В одной семье было много детей. Семеро из них любили капусту, шестеро любили морковь, пятеро - горох. Четверо из детей любили капусту и морковь, трое любили капусту и горох, двое - морковь и горох, а один - и капусту, и морковь, и горох. Сколько было детей в этой семье?

Ответ

10 детей.

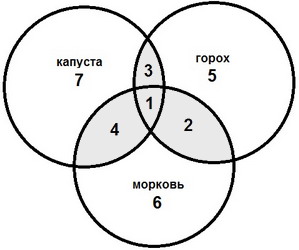
Решение задачи

По условию задачи в семье 7 детей любили капусту, 6 - морковь и 5 - горох. Просуммируем известные величины: 7+6+5=18. В этой сумме дети, которые любят сразу несколько овощей учтены дважды. 4 ребенка любили капусту и морковь, 3 - капусту и горох, а 2 - морковь и горох. Следовательно: 18-4-3-2=9 детей. Известно, что один ребенок ест все овощи. Он сначала был включен в сумму 3 раза как любитель каждого овоща, потом исключен также 3 раза. Поэтому его нужно добавить в сумму: 9+1=10 детей. Таким образом, в семье было 10 детей.

О задаче

Категория: Множества, Принцип Дирихле,
Степень сложности: сложная.
Ключевые слова: 1, 2, 3, 4, 5, 6, 7, горох, капуста, морковь, ребенок, семья,
Источник: Математическая шкатулка,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Физик, устав, лег спать в десять часов вечера; предварительно он завел будильник на 12 часов следующего дня. Сколько часов он успеет проспать, прежде чем будильник его разбудит?

a) 14 часов
b) 12 часов
c) 2 часа
d) 6 часов