Палку ломают случайным образом на 3 части.

Палку случайным образом ломают на три части; какова вероятность того, что из обломков можно составить треугольник? (Точки перелома равномерно распределены по длине палки)

Ответ

1/4

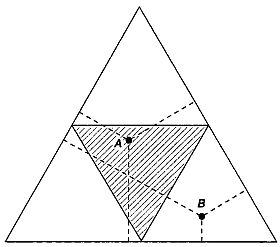
Решение задачи

Действительно, нарисуем равносторонний треугольник и соединим середины его сторон отрезками прямых. У нас получится равносторонний треугольник меньших размеров, расположенный внутри первого (на рисунке меньший треугольник заштрихован). Сумма длин перпендикуляров, опущенных из любой точки большого треугольника на его стороны, не зависит от выбора точки и равна высоте большого треугольника. Если эту точку выбрать внутри меньшего треугольника (на рисунке этому условию удовлетворяет точка А), то любой из трех перпендикуляров будет не больше суммы двух других перпендикуляров. Следовательно, из отрезков, равных по длине трем перпендикулярам, опущенным из любой точки малого треугольника на стороны большого, всегда можно построить треугольник. Если же точка лежит вне малого треугольника (на рисунке - точка В), то один перпендикуляр заведомо длиннее суммы двух других перпендикуляров, и построить из таких перпендикуляров треугольник невозможно. Так как площадь заштрихованого треугольника составляет 1/4 площади всего треугольника, то искомая вероятность равна 1/4. Таким образом, если палку разломать на три части, то из ее обломков можно составить треугольник с вероятностью 1/4 (25%).

О задаче

Категория: Задачи на вероятность, Геометрические задачи,
Степень сложности: сложная.
Ключевые слова: 3, палка, треугольник,
Источник: Математические головоломки и развлечения,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Володя купил несколько яблок и принес их домой. Сестра спросила его:
- Сколько ты уплатил за яблоки?
Володя ответил:
- А вот угадай. Я купил в 4 раза больше яблок, но платил вдвое меньше за каждое яблоко, чем ты вчера.
Сколько денег уплатил Володя, если сестра его истратила накануне на яблоки 75 коп.?

a) 1 руб.
b) 1 руб. 50 коп.
c) 2 руб. 75 коп.
d) 1 руб. 25 коп.