Изуродованная шахматная доска.

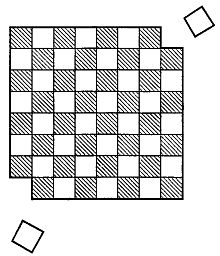
Для этой задачи потребуются шахматная доска и 32 кости домино. Размер каждой кости должен быть таким, чтобы она закрывала ровно две клетки доски, тогда 32 костями можно покрыть все 64 клетки. Предположим теперь, что две угловые клетки, расположенные на концах "белой" диагонали выпилены и одной кости домино нет. Можно ли так расположить оставшуюся 31 кость, чтобы они полностью покрыли все 62 клетки изуродованной шахматной доски?

Ответ

Нельзя.

Решение задачи

Разместить 31 кость домино на доске, у которой вырезаны два угловых квадрата на противоположных концах диагонали, невозможно. Доказательство этого факта неожиданно просто. Две диагонально противоположные клетки должны быть одного цвета. Поэтому, если их вырезать, клеток одного цвета на доске останется на две больше, чем другого. Каждая кость домино может прикрыть два квадрата разного цвета, поскольку только такие квадраты примыкают друг к другу. После того как 30 костей закроют 60 клеток доски, свободными останутся два квадрата одинакового цвета. Они не могут находиться рядом, и поэтому их нельзя прикрыть последней костью домино.

О задаче

Категория: Логические задачи, Шахматные задачи, Инвариант,
Степень сложности: средняя.
Ключевые слова: 31, 32, 62, 64, домино, шахматы,
Источник: Математические головоломки и развлечения, Математическая шкатулка, Очерки о математических задачах на смекалку,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Разложим 10 монет в виде треугольника, как показано на рисунке. Задача заключается в том, чтобы, передвигая по одной монете, перевернуть треугольник - обратить его вершиной вниз. Новое положение каждой монеты должно однозначно определяться точками ее касания с двумя другими монетами. Чему равно минимальное число ходов, которые необходимо совершить для опрокидывания треугольника?

a) 4
b) 5
c) 3
d) 6