|
|
Ряды
Числовые ряды - одно из центральных понятий математического анализа. В простейшем случае ряд записывается как бесконечная сумма чисел. Характерным примером задачи на ряды является задача о прыгающем мяче, которую можно найти во многих сборниках задач на смекалку.
Список занимательных задач в категории "Ряды"
Ахиллес и черепаха.старинная задача, задача на движение, задача на ряды
Ахиллес и черепаха бегут наперегонки. Черепаха получает фору, скажем, 100 м. Мы примем, что Ахиллес бежит в десять раз быстрее черепахи. Когда он пробежит 100 м форы, черепаха будет в 10 м впереди него. Когда Ахиллес пробежит эти 10 м, черепаха будет от него в 1 м. Когда Ахиллес оставит за собою этот метр, черепаха уйдет вперед на 10 см. И так далее. Черепаха будет впереди на 1 см, на 1 мм и т. д., но будет все же впереди на расстоянии, превышающем нуль. Ахиллес никогда не догонит черепаху?
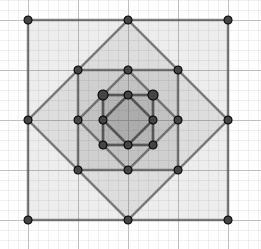
Бесконечная последовательность квадратов.геометрическая задача, задача на ряды
На рисунке изображена бесконечная последовательность квадратов, вписанных друг в друга таким образом, что вершины каждого последующего квадрата совпадают с серединами сторон предыдущего квадрата. Сторона самого большого квадрата имеет единичную длину. Чему равна площадь всей бесконечной последовательности квадратов?
Задача про Ахиллеса и черепаху.старинная задача, задача на движение, задача на ряды
Предположим, что Ахиллес бежит со скоростью, всемеро превышающей скорость черепахи, которая и на этот раз имеет 100 метров форы. Сколько придется пробежать Ахиллесу, прежде чем он догонит черепаху?
Задача про бесконечный отель.логическая задача, задача на ряды
Как поселить в отель с бесконечным количеством комнат, в каждой из которых уже находится постоялец, еще одного постояльца?
Задачи о прыгающем мяче.задача на ряды
Предположим, что идеально круглый мяч, падая с высоты 1 м, каждый раз подпрыгивает на высоту, составляющую 1/3 от предыдущей. Если бы каждый подскок длился 1 секунду, мяч прыгал бы вечно. Однако времена подскоков убывают вместе с высотой, образуя сходящийся ряд, поэтому мяч в конце концов перестает тодпрыгивать, хотя (теоретически) успевает совершить бесконечное число подскоков. Определить путь, который успевает пройти идеальный мяч, прежде чем он окончательно перестанет подпрыгивать.
Парадокс Гранд отель.логическая задача, задача на ряды
Как поселить в отель с бесконечным количеством комнат, в каждой из которых уже находится постоялец, еще одного постояльца?
Парадокс Зенона.старинная задача, задача на движение, задача на ряды
Ахиллес и черепаха бегут наперегонки. Черепаха получает фору, скажем, 100 м. Мы примем, что Ахиллес бежит в десять раз быстрее черепахи. Когда он пробежит 100 м форы, черепаха будет в 10 м впереди него. Когда Ахиллес пробежит эти 10 м, черепаха будет от него в 1 м. Когда Ахиллес оставит за собою этот метр, черепаха уйдет вперед на 10 см. И так далее. Черепаха будет впереди на 1 см, на 1 мм и т. д., но будет все же впереди на расстоянии, превышающем нуль. Ахиллес никогда не догонит черепаху?
Пизанская башня.задача на ряды
Если уронить мячик с падающей Пизанской башни на высоте 179 футов над землей и если при каждом отскоке этот мячик будет подниматься ровно на 1/10 предыдущей высоты, то какое расстояние он проделает, прежде чем ляжет на землю?
Сколько пролетит мячик?задача на ряды
Если уронить мячик с падающей Пизанской башни на высоте 179 футов над землей и если при каждом отскоке этот мячик будет подниматься ровно на 1/10 предыдущей высоты, то какое расстояние он проделает, прежде чем ляжет на землю?
Тебе отсюда не дойти вот до того дерева.задача на движение, задача на ряды
- Тебе отсюда не дойти вот до того дерева, - сказал Володя Пете и хитро улыбнулся.
- Опять какая-нибудь шутка или фокус, - ответил Петя, стараясь про себя отгадать, что задумал его друг.
- Никакая не шутка, а строгий математический расчет. Слушай, когда ты пройдешь половину расстояния от нас до дерева, то тебе останется пройти еще столько же, то есть такую же половину, а когда ты пройдешь еще половину оставшегося пути, то тебе снова останется пройти еще половину; и, сколько бы ты ни шел, тебе все-таки будет нужно пройти еще половину. Иначе говоря, ты пройдешь сперва 1/2 пути, затем 1/4 далее 1/8, 1/16, 1/32 и т.д., то есть ты будешь подходить все ближе и ближе к дереву, но так и не дойдешь до него!
В чем ошибка "доказательства" Володи?
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Задачи на внимательность |
 Задачи с подвохом |
 Эффект плюс-минус один |
 Логические задачи |
 Задачи со спичками |
 Задачи с шестеренками |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |