≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Задачи про серебро

Список занимательных задач про серебро

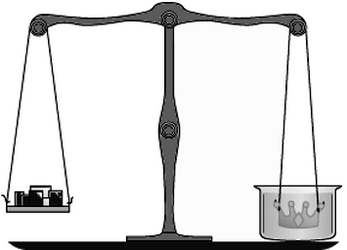
Задача Архимеда.
задача на взвешивание, старинная задача
Гиерон поручил мастеру изготовить венец для одной статуи и приказал выдать ему необходимое количество золота и серебра. Когда венец был доставлен, взвешивание показало, что он весит столько же, сколько весили вместе выданные золото и серебро. Однако правителю донесли, что мастер утаил часть золота, заменив его серебром. Гиерон призвал Архимеда и предложил ему определить, сколько золота и сколько серебра заключает изготовленная мастером корона. Архимед решил эту задачу, исходя из того, что чистое золото теряет в воде 20-ю долю своего веса, а серебро - 10-ю. Если вы желаете испытать свои силы на подобной задаче, примите, что мастеру было отпущено 8 кг золота и 2 кг серебра и что, когда Архимед взвесил корону под водой, она весила не 10, а всего 9¹/₄ кг. Попробуйте определить по этим данным, сколько золота утаил мастер. Венец был изготовлен из сплошного металла, без пустот.

Монета в миллион рублей.
геометрическая задача
Вообразите серебряную монету в миллион рублей, которая имеет ту же форму, что и рублевая монета (имееься в виду серебрянная монета 1 рубль 1921 года, диаметром 33,5 мм). Какого, примерно, диаметра была бы такая монета? Если бы ее поставить на ребро рядом с вашим домом, то во сколько раз она была бы выше его?

Задача про 12 мешков с монетами.
задача на взвешивание
12 мешков заполнены серебряными монетами. Одна монета весит 1 фунт (16 унций). В одном из мешков каждая монета содержит на целую унцию меньше серебра, чем положено. Как при помощи достаточно точных весов за одно взвешивание, определить в котором из двенадцати мешков содержатся облегченные монеты?

Двугривенный весит вдвое больше чем гривенник.
старинная задача, задача с подвохом
Двугривенный весит вдвое больше, чем гривенник, серебра в нем вдвое больше и стоит он вдвое дороже. Что же дороже: килограмм гривенников или полкилограмма двугривенных?

Имеется 9 слитков золота и 11 слитков серебра.
задача на взвешивание, старинная задача
Имеется 9 слитков золота и 11 слитков серебра, их взвесили, вес как раз совпал. Переложили слиток золота и слиток серебра, золото стало легче на 13 ланов. Спрашивается, каков вес слитка золота и слитка серебра каждого в отдельности.

К хозяину гостиницы однажды пришел постоялец, не имевший денег.
занимательная задача
К хозяину гостиницы однажды пришел постоялец, не имевший денег, но обладавший серебряной цепочкой, состоящей из семи звеньев. Хозяин согласился держать этого постояльца неделю, при условии, что тот будет ему ежедневно отдавать в виде платы одно из звеньев цепочки. Какое наименьшее число звеньев надо распилить для того, чтобы владелец цепочки смог ежедневно в течение семи дней расплачиваться с хозяином (быть может, забирая у него при этом отданные ранее звенья и выдавая взамен их другие)?

◄ На предыдущую страницу