|
|
Задачи про остров
Список занимательных задач про остров
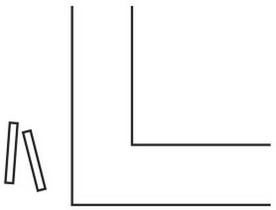
Задача про ров и две доски.задача о переправе, геометрическая задача
Четырехугольное поле окружено рвом, ширина которого всюду одинакова. Даны две доски, длина каждой из которых равна точно ширине рва, и требуется с помощью этих досок устроить переход через ров.
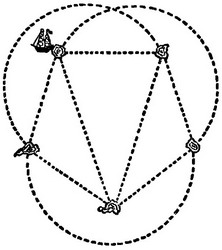
Пять островов.комбинаторная задача, задача с перестановками, задача на графы
На рисунке изображена карта с пятью островами. Каждый год корабль ходит по всем десяти указанным путям, но никогда в один и тот же год не ходит ни по одному пути дважды. Сколькими различными способами корабль сможет совершить эти десять ежегодных плаваний, отправляясь всегда от одного и того же острова и заканчивая плавание на том же острове, откуда впервые отчалил?
Ледокол и самолет.задача на движение
Ледокол вышел из морского порта по направлению к острову, который отстоит от этого порта на расстоянии 840 км, и плыл со скоростью 20 км в час. Ледокол имел на своем борту самолет. В некотором расстоянии от места назначения самолет был спущен на воду и вылетел по направлению к острову со скоростью 120 км в час. Сколько времени пробыл самолет в воздухе, если известно, что летчик, управлявший самолетом, пробыл в пути всего 22 часа, считая с момента отплытия ледокола из порта и до прибытия самолета на остров?
Какой вопрос задал путешественник?логическая задача
Однажды путешественник оказался на острове, который населяли племя лжецов и племя правдивых туземцев. Члены первого племени всегда лгали, члены второго - всегда говорили только правду. Путешественник дошел до места, где дорога раздваивалась, и вынужден был спросить у оказавшегося поблизости туземца, какая из двух дорог ведет в деревню. Узнать, кем был встреченный туземец - лжецом или правдивым человеком, - путешественник не мог. Все же, поразмыслив, логик задал ему один-единственный вопрос и, получив ответ, узнал, по какой дороге следует идти. Какой вопрос задал путешественник?
Кругосветный полет.задача на максимум и минимум
Группа самолетов базируется на небольшом острове. Баки каждого самолета вмещают столько топлива, что его хватает на облет половины земного шара. При заправке в воздухе из баков одного самолета в баки другого можно перекачивать любое количество горючего. На земле заправку можно производить только на острове. Для удобства решения задачи предполагается, что заправка на земле и в воздухе происходит мгновенно, бех потерь времени. Чему равно минимальное число самолетов, которые смогут обеспечить полет одного самолета по большому кругу, если считать, что скорость и расход топлива у всех самолетов одинаковы и все самолеты благополучно возвращаются на свою базу?
Мартышка и кокосовые орехи.задача на прогрессию
Пять матросов и мартышка потерпели кораблекрушение и высадились на необитаемом острове. Весь первый день они занимались сбором кокосовых орехов. Вечером они сложили все орехи в кучу и легли спать. Ночью, когда все заснули, один из матросов, подумав, что утром при разделе орехов может вспыхнуть ссора, встал, чтобы взять свою долю орехов немедля. Он разделил все кокосовые орехи на пять равных кучек, а один оставшийся орех отдал мартышке. Затем матрос спрятал свою долю, а все остальные орехи снова сложил в одну кучу. Через некоторое время проснулся другой "робинзон" и сделал то же самое. У него тоже остался один лишний орех, и он отдал его мартышке. И так один за другим поступили все пятеро потерпевших кораблекрушение. Каждый из них взял себе одну пятую орехов из той кучи, которую он нашел при пробуждении, и каждый отдал один орех мартышке. Утром они поделили оставшиеся орехи, и каждому досталось поровну - по одной пятой. Разумеется, каждый из матросов не мог не знать, что части орехов не хватает, но так как у каждого из них совесть была одинаково нечиста, то никто ничего не сказал. Сколько кокосовых орехов было первоначально?
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Задачи на внимательность |
 Задачи с подвохом |
 Эффект плюс-минус один |
 Логические задачи |
 Задачи со спичками |
 Задачи с шестеренками |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |