≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Задачи с цифрой 1

Продолжение списка занимательных задач с цифрой 1 (страница 25)

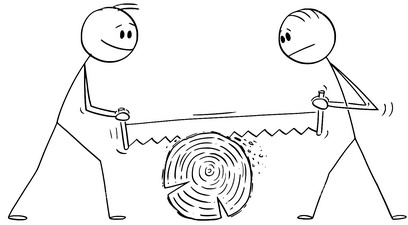
Сто метровых бревен были распилены пополам за один день.
эффект плюс-минус один, задача на разрезание
Сто метровых бревен были распилены пополам за один день. За сколько дней будут распилены сто трехметровых бревен на полуметровые чурки?

В воскресенье в 6 часов утра на гладкий столб высотой в 11 метров вползла гусеница.
эффект плюс-минус один
В воскресенье в 6 часов утра на гладкий столб высотой в 11 метров вползла гусеница и стала подниматься. Гусеница ползла равномерно и так, что за первую половину суток она поднималась на 3 метра, а за вторую половину суток опускалась на 1 метр. В какой день и час гусеница достигнет верха столба?

Трое мужчин попросили мальчика сходить в магазин.
задача с подвохом
Трое мужчин попросили мальчика сходить в магазин и купить им торт. Каждый из мужчин дал мальчику 1 рубль. Мальчик скоро вернулся, принес торт и 50 коп. сдачи. Мальчику дали 20 коп. на мороженое, а по 10 коп. взял каждый из мужчин. Таким образом, всего денег было 3 рубля; так как каждый из мужчин получил по 10 коп. сдачи, то, фактически, все трое заплатили за торт 90 коп. × 3 = 2 рубля 70 коп.; кроме того, мальчику дали 20 коп., - значит, всего истрачено 2 рубля 70 коп. + 20 коп. = 2 рубля 90 коп. Куда девались 10 копеек?

Двое друзей захотели позавтракать и достали свои лепешки.
занимательная задача
Двое друзей захотели позавтракать и достали свои лепешки: у одного их было 5, а у другого - 3. Подошел третий и попросил разрешения разделить с ними трапезу. Все трое, съев 8 лепешек, получили одинаковые порции. Третий заплатил 8 рупий и ушел, а двое стали делить деньги.
- Ты и я съели поровну, - сказал первый, - следовательно, и деньги нам нужно разделить поровну.
- Нет, - возразил второй. - Ведь у меня было 5 лепешек, а у тебя только 3. Значит, я должен взять 5 рупий, а ты - 3.
Но первый не согласился, и оба пошли к судье.
Судья решил спор так: все трое съели поровну, - рассуждал он, - значит, каждую лепешку вы делили на три части; и всех частей получилось 24. На долю каждого пришлось 8 частей. Из трех лепешек вышло 9 частей, но при этом 8 частей съел хозяин этих трех лепешек. Следовательно, он должен получить только 1 рупию, а тот, у кого было 5 лепешек, должен получить 7 рупий.
Кто же здесь прав?

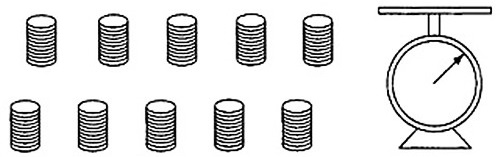
Сто копеечных монет разложены на десять кучек.
задача на взвешивание
Сто копеечных монет разложены на десять кучек, по 10 монет в каждой кучке. Как известно, одна копеечная монета весит 1 г. От времени и частого употребления монеты могут стираться и немного терять в весе. И вот одна из десяти кучек состоит из десяти монет, каждая из которых весит по 0,9 г. Как всего за одно лишь взвешивание на точных весах можно выявить эту кучку более легких монет?

Как разделить циферблат часов на 2 части?
задача с часами, магический квадрат
Как разделить циферблат часов одной прямой линией на две части так, чтобы в каждой части сумма цифр была одинакова.

На 1 минуту быстрее.
задача на движение
Автомобиль едет со скоростью 60 км/ч. Водитель хочет проезжать каждый километр на 1 минуту быстрее. На сколько ему следует увеличить скорость?

Перепутанные таблички.
логическая задача
Представьте себе, что у вас есть три коробки. В одной лежат два черных шара, во второй - два белых и в третьей - один черный шар и один белый. На коробках в соответствии с их содержимым были надписи ЧЧ, ЧБ и ББ, но кто-то их перепутал, и теперь на каждой коробке стоит надпись, не соответствующая содержимому. Чтобы узнать, какие шары лежат в каждой из трех коробок, разрешается вынимать по одному шару из коробки и, не заглядывая внутрь, возвращать его обратно. Какое минимальное число шаров нужно вынуть, чтобы с уверенностью определить содержимое всех коробок?

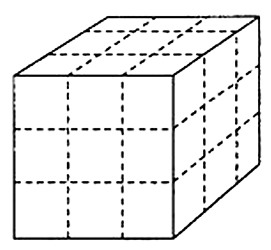
Распиливание куба.
задача на разрезание, геометрическая задача
Один плотник решил распилить кубик размером 3×3×3 см на 27 кубиков с ребром в 1 см. Это делается очень просто: надо распилить куб по шести плоскостям, не разнимая его при этом на куски. Можно ли уменьшить число распилов, если после каждого из них складывать отпиленные части по-новому?

Фальшивые монеты.
задача на взвешивание
Имеется 10 кучек монет, по 10 монет в каждой. Одна из кучек целиком состоит из фальшивых монет, но какая именно - неизвестно. Известен лишь вес настоящей монеты, и, кроме того, установлено, что каждая фальшивая монета на один грамм тяжелее, чем нужно. Монеты можно взвешивать на пружинных весах. Какое минимальное число взвешиваний необходимо произвести, чтобы отыскать кучку, целиком состоящую из фальшивых монет?

Продолжение списка задач с цифрой 1:

◄ Назад 21 22 23 24 25 Вперёд ►

◄ На предыдущую страницу