|
|
Задачи про стрелки
Список занимательных задач про стрелки
Часы бьют каждый час и отбивают столько ударов сколько показывает часовая стрелка.задача с часами, старинная задача, задача на прогрессию
Часы бьют каждый час и отбивают столько ударов, сколько показывает часовая стрелка. Сколько ударов отобьют часы в течении 12 часов?
Один человек спросил который час.задача с часами, старинная задача
Один человек спросил: - Который час? Ему ответили, что часовая и минутная стрелка совмещены и находятся на одной линии между 9 и 10 часами утра. Сколько было времени?
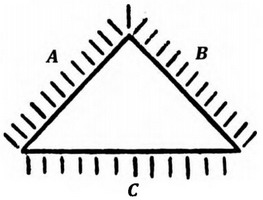
Тридцать шесть актеров сидят в гостинице за тремя столамизанимательная задача
36 актеров сидят в гостинице за тремя столами А, В и С, образующими треугольник, по 12 человек за каждым, и пируют до тех пор, пока не замечают, что у них не хватит денег для уплаты по счету. Тогда они просят хозяина присоединиться к компании и занять место у одного из углов треугольника. Веселье продолжается еще некоторое время, а затем комик Феликс предлагает превратить скучную процедуру расчета в аттракцион: расплатится тот, кто останется после определенной считалки, которая будет вестись по часовой стрелке. Каждый седьмой может уйти, а последний оставшийся заплатит за всех. Когда все приступили к игре, актеры выбыли один за другим, а платить по счету выпало на долю обманутого хозяина. Где сидел Феликс, с которого начался счет?
В 12 часов дня часовая и минутная стрелка совпадают. В 12 часов дня часовая и минутная стрелки часов совпадают. Через сколько минут после этого они снова совпадут?задача с часами
Сколько есть положений на часах когда часовая и минутная стрелки совмещаются?задача с часами, старинная задача
Часы пробили полночь. Сколько раз до следующей полуночи часовая и минутная стрели будут совмещаться?
Стрелки часов.задача с часами
Определите момент между 1 часом и двумя часами, когда минутная стрелка покрывает часовую (стреки совмещены).
Через какое время минутная стрелка догонит часовую?задача с часами
Через сколько минут после того, как часы показывали 4 ч, минутная стрелка догонит часовую стрелку?
Длина минутной стрелки часов на Спасской башне Московского Кремля 3.5 м.геометрическая задача, задача с часами
Длина минутной стрелки часов на Спасской башне Московского Кремля 3.5 м. Какой путь опишет ее конец за сутки?
Сколько раз в сутки часовая и минутная стрелки образуют прямой угол?геометрическая задача, задача с часами
Сколько раз в сутки стрелки часов (часовая и минутная) оказываются перпендикулярными друг другу?
Задача для Эйнштейна.задача с часами
Возьмем положение стрелок в 12 часов. Если бы в этом положении большая и малая стрелки обменялись местами, они дали бы все же правильные показания. Но в другие моменты, - например, в 6 часов, взаимный обмен стрелок привел бы к абсурду, к положению, какого на правильно идущих часах быть не может: минутная стрелка не может стоять на 6, когда часовая показывает 12. Возникает вопрос: как часто стрелки часов занимают такие положения, при которых замена одной стрелкой другою дает новое положение, тоже возможное на правильных часах?
Продолжение списка задач про стрелки:
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Прогрессии |
 Комбинаторика |
 Задачи с перестановками |
 Графы |
 Принцип Дирихле |
 Множества |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |