Задача для Эйнштейна.

Возьмем положение стрелок в 12 часов. Если бы в этом положении большая и малая стрелки обменялись местами, они дали бы все же правильные показания. Но в другие моменты, - например, в 6 часов, взаимный обмен стрелок привел бы к абсурду, к положению, какого на правильно идущих часах быть не может: минутная стрелка не может стоять на 6, когда часовая показывает 12. Возникает вопрос: как часто стрелки часов занимают такие положения, при которых замена одной стрелкой другою дает новое положение, тоже возможное на правильных часах?

Ответ

143 решения.

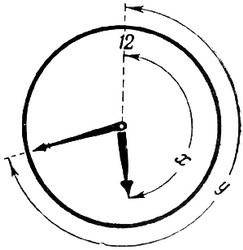
Решение задачи

Эту задачу предложил известному физику Альберту Эйнштейну его биограф и друг Александр Мошковский, желая развлечь своего приятеля во время болезни.
Будем измерять расстояния стрелок по кругу циферблата от точки, где стоит цифра 12, в 60-х долях окружности. Пусть одно из требуемых положений стрелок наблюдалось тогда, когда часовая стрелка отошла от цифры 12 на х делений, а минутная - на у делений. Так как часовая стрелка проходит 60 делений за 12 часов, т. е. 5 делений в час, то х делений она прошла за x/5 часов. Иначе говоря, после того как часы показывали 12, прошло x/5 часов. Минутная стрелка прошла у делений за у минут, т. е. за y/60 часов. Иначе говоря, цифру 12 минутная стрелка прошла y/60 часов тому назад, или через x/5 - y/60 часов после того, как обе стрелки были на двенадцати. Это число является целым (от нуля до 11), так как оно показывает, сколько полных часов прошло после двенадцати. Когда стрелки обменяются местами, мы найдем аналогично, что с двенадцати часов до времени, показываемого стрелками, прошло y/5 - x/60 полных часов. Это число также является целым (от нуля до 11). Имеем систему уравнений: 1. x/5 - y/60 = m; 2. y/5 - x/60 = n, где m и n - целые числа, которые могут меняться от 0 до 11. Из этой системы находим: x = 60(12m + n)/143, y = 60(12n + m)/143. Давая тип значения от 0 до 11, мы определим все требуемые положения стрелок. Так как каждое из 12 значений m можно сопоставлять с каждым из 12 значений n, то, казалось бы, число всех решений равно 12 × 12 = 144. Но в действительности оно равно 143, потому что при m = 0, n = 0 и при m = 11, n = 11 получается одно и то же положение стрелок. Таким образом, число всех моментов, удовлетворяющих условию задачи, 143.

О задаче

Категория: Задачи с часами,
Степень сложности: сложная.
Ключевые слова: 6, 12, время, Мошковский Александр, стрелка, часы, Эйнштейн Альберт,
Источник: Занимательная алгебра, Самые знаменитые головоломки мира,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Чайник вскипел, и только успели налить два стакана чаю, как от соседей прибежал мальчик. Он сказал, что сейчас по телевизору начнется интересная передача. Все, кто собирался пить чай, ушли к соседям. В каком из стаканов чай остынет скорее?

a) Остынут одновременно.
b) В стакане с ложкой скорее.
c) В стакане без ложки скорее.