≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Задачи про круг

Продолжение списка занимательных задач про круг (страница 4)

Определить приближение для числа Пи.
старинная задача
Периметр квадрата, описанного около круга, на четверть его больше окружности этого круга. Определить приближение для числа Пи, которым в данном случае пользовались евреи.

Девять кружков.
задача на разрезание
Как зачеркнуть девять кружков четырьми прямыми линиями, не отрывая руки.

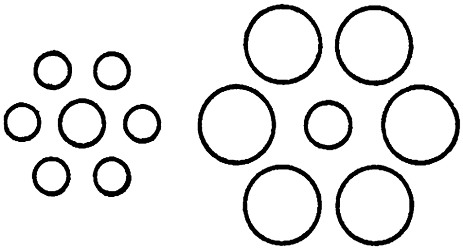
Какой круг больше?
задача на внимательность, задача с подвохом
В какой фигуре центральный круг больше: в левой или в правой?

На какое наибольшее число частей можно разрезать круг шестью прямыми?
задача на разрезание, геометрическая задача
Попробуйте рассечь круг шестью прямыми линиями на наибольшее возможное число частей.

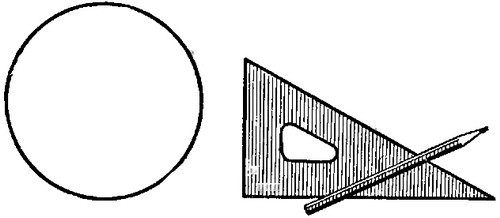
Как найти центр окружности?
геометрическая задача
Как найти центр окружности при помощи чертежного треугольника без делений и карандаша?

Задача про точильный круг.
геометрическая задача
Два человека, сложив свои сбережения, купили точильный круг. Поскольку они жили в нескольких милях друг от друга, то решили, что сначала кругом будет пользоваться старший из владельцев, а когда круг уменьшится ровно вдвое, он передаст его второму компаньону. Круг имел в диаметре ровно 22 дюйма, в середине его имелось отверстие для оси диаметром 3¹/₇ дюйма. Чему должен равняться диаметр круга, когда его получит второй компаньон?

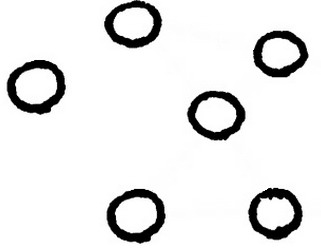
Перенесите один кружок, чтобы провести четыре прямые.
задача на внимательность
Сейчас можно провести только две прямые через три кружка. Необходимо стереть один из кружков и нарисовал его в другом месте так, чтобы можно было провести четыре прямые через три кружка.

Сколько частей можно получить с помощью шести разрезов?
задача на разрезание, геометрическая задача
Тетушка Мэри попросила повара разрезать пирог на максимальное число частей шестью прямыми разрезами ножа. Чему, по-вашему, равно это число?

Сторона клетки на шахматной доске 4 см.
задача на шахматной доске, геометрическая задача
Сторона клетки на шахматной доске 4 см. Чему равен радиус наибольшей окружности, которую можно провести на шахматной доске (не выходя за ее границы) так, чтобы она проходила только по черным клеткам?

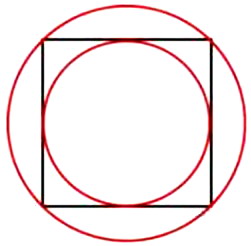
Описанный круг по площади вдвое больше вписанного.
старинная задача, геометрическая задача
Архимед утверждал, что если круг описан около квадрата, а другой в него вписан, то описанный круг по площади вдвое больше вписанного. Так ли это?

Продолжение списка задач про круг:

1 2 3 4 5

◄ На предыдущую страницу