Тетраэдр в кубе.

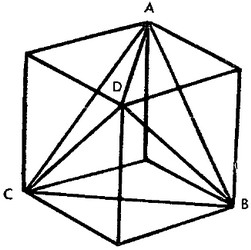
На рисунке изображен наибольший тетраэдр, содержащийся в некотором кубе. Ребро куба имеет длину 1, так что длина ребра у тетраэдра равна √2. Определите объем тетраэдра АВСD.

Ответ

1/3

Решение задачи

Забудем на минуту о тетраэдре и сосредоточим внимание на четырех равных треугольных пирамидах, которые останутся, если наш тетраэдр удалить из куба (вершины этих пирамид совпадают с неотмеченными вершинами куба). Возьмем одну из них, образованную треугольником СВD и нижней вершиной куба. Объем пирамиды равен произведению 1/3 основания на высоту. Основанием нашей пирамиды служит треугольник, площадь которого равна половине площади основания куба, то есть равна 1/2; высота же ее равна 1. Таким образом,'объем нашей пирамиды равен 1/6. Суммарный объем 4 таких пирамид составляет 2/3. Следовательно, на долю тетраэдра остается 1/3.

О задаче

Категория: Геометрические задачи,
Степень сложности: средняя.
Ключевые слова: 1, куб, объем, тетраэдр,
Источник: Россыпи головоломок,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Две богомолки отправились из Москвы в Троице-Сергиеву лавру. Обе они прошли 60 верст. Сколько верст прошла каждая, если шли они с одинаковой скоростью?

a) 60 верст.
b) 90 верст
c) 120 верст.
d) 30 верст