|
|
Задачи про число Пи
Список занимательных задач про число Пи
Ошибка в числе Пи.геометрическая задача, задача с процентами
Определить величину относительной ошибки, какая происходит, когда при вычислении длины окружности принимают π=3.
Число Пи как корень из 10.задача с процентами, старинная задача
У одного древнего индусского математика (Брахмагупта, VII век нашей эры) указано для π значение √10. Насколько это отличается от 3,14; определите величину отклонения в %.
Площадь круга.геометрическая задача
В древней египетской рукописи (папирус Ринда/Ахмеса) площадь круга равна площади квадрата, сторона которого составляет 8/9 диаметра круга. Определите относительную ошибку такого расчета в процентах принимая π=3,14.
Число Пи в Древнем Вавилоне.геометрическая задача, старинная задача
За длину окружности вавилоняне принимали периметр вписанного в эту окружность правильного шестиугольника. Найти приближение для числа Пи, которым пользовались вавилоняне.
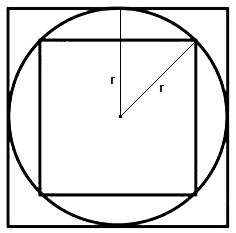
Число Пи в Древнем Египте.геометрическая задача, старинная задача
Египтяне, заменяя площадь круга площадью равновеликого квадрата, брали за сторону последнего 8/9 диаметра круга.Найти приближение для числа Пи, которым пользовались египтяне.
Правило Катнайаны.старинная задача
Катиайана говорит, что надо разделить диаметр круга на 15 равных частей и взять 13 таких частей для стороны квадрата примерно равного кругу. Оценить в процентах ошибку для числа Пи (3,1415) при указанных расчетах.
Определить приближение для числа Пи.старинная задача
Периметр квадрата, описанного около круга, на четверть его больше окружности этого круга. Определить приближение для числа Пи, которым в данном случае пользовались евреи.
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Геометрические задачи |
 Задачи на разрезание |
 Задачи на взвешивание |
 Задачи на переливание |
 Задачи о переправе |
 Шахматные задачи |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |