≡
А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я #
§🔍

Задачи Древней Греции

Список занимательных задач Древней Греции

Три грации имели по одинаковому числу плодов.
старинная задача
Три грации имели по одинаковому числу плодов и встретили девять муз. Каждая из граций отдала каждой из муз по одинаковому числу плодов. После этого у каждой из муз и каждой из граций стало по одинаковому числу плодов.Сколько плодов было у каждой из граций до встречи с музами?

Яблоко раздора.
логическая задача, старинная задача
Древнегреческие богини Гера, Афродита и Афина пришли к юному Парису, чтобы тот решил, кто из них прекраснее. Представ перед Парнасом, богини высказали следующие утверждения:

1. Афродита: Я самая прекрасная.
2. Афина: Афродита не самая прекрасная.
3. Гера: Я самая прекрасная.
4. Афродита: Гера не самая прекрасная.
5. Афина: Я самая прекрасная.

Парис, прилегший отдохнуть, не счел нужным даже снять платок, прикрывавший глаза от яркого солнца. Он предположил, что все утверждения прекраснейшей из богинь - истинны, а все утверждения двух остальных - ложны. Мог ли Парис вынести решение, кто прекраснее из богинь, только на основании их слов?

У Пифагора однажды спросили сколько у него учеников.
старинная задача
Однажды у Пифагора спросили, сколько у того учеников, на что древнегречески математик и философ ответил следующее: - Половина моих учеников изучает прекрасную математику, четверть исследует тайны вечной природы, седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей. Столько учеников веду я к рождению вечной истины. Сколько учеников было у Пифагора?

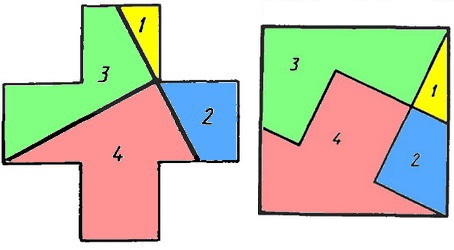
Крест.
задача на разрезание, старинная задача
Древние греки на хлебе изображали крест, считая его символом жизни. Попробуйте разрезать крест на четыре части и сложить из получившихся частей квадрат.

На памятнике древнегреческому математику Диофанту имеется надпись.
задача про возраст, старинная задача
Диофант Александрийский - выдающийся древнегреческий математик. По преданию, эпитафия на его могильном камне была написана в виде задачи:

Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости.
Шестую часть долгой жизни он был ребенком, двенадцатую - юношей, седьмую - провел неженатым.
Через пять лет после женитьбы у него родился сын, который прожил вдвое меньше отца.
Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый его близкими.
Скажи, если умеешь считать, сколько лет прожил Диофант?

Который час, Пифагор?
задача с часами, старинная задача
Рассказывают, что некто при встрече с греческим философом и математиком Пифагором спросил того:
- Который час? Пифагор ответил:
- До конца суток осталось дважды две пятых того, что уже прошло от начала.
Который был час?

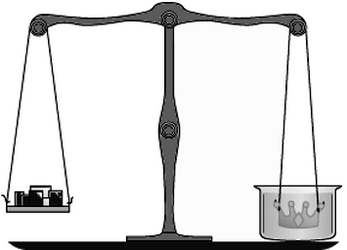
Задача Архимеда.
задача на взвешивание, старинная задача
Гиерон поручил мастеру изготовить венец для одной статуи и приказал выдать ему необходимое количество золота и серебра. Когда венец был доставлен, взвешивание показало, что он весит столько же, сколько весили вместе выданные золото и серебро. Однако правителю донесли, что мастер утаил часть золота, заменив его серебром. Гиерон призвал Архимеда и предложил ему определить, сколько золота и сколько серебра заключает изготовленная мастером корона. Архимед решил эту задачу, исходя из того, что чистое золото теряет в воде 20-ю долю своего веса, а серебро - 10-ю. Если вы желаете испытать свои силы на подобной задаче, примите, что мастеру было отпущено 8 кг золота и 2 кг серебра и что, когда Архимед взвесил корону под водой, она весила не 10, а всего 9¹/₄ кг. Попробуйте определить по этим данным, сколько золота утаил мастер. Венец был изготовлен из сплошного металла, без пустот.

Парадокс парикмахера.
логическая задача, старинная задача, задача на инвариант
В некоторой деревне, в которой живет один единственный парикмахер, был издан указ: парикмахер имеет право брить тех и только тех жителей деревни, которые не бреются сами. Вопрос: Может ли парикмахер брить самого себя?

Как число 100 разделить два раза?
старинная задача, числовая головоломка
Требуется число 100 разделить два раза так, чтобы большая часть от первого деления была вдвое более меньшей части от второго деления и чтобы большая часть от второго деления была втрое больше меньшей части от первого деления.

Задача Метродора.
старинная задача, задача на дроби
Корона весит 60 персидских мин и состоит из сплава золота, меди, олова и железа. Золото и медь составляют вместе 2/3, золото и олово 3/4, золото и железо 3/5 общего веса. Определить вес каждого металла в отдельности.

Продолжение списка задач Древней Греции:

1 2

◄ На предыдущую страницу