Числовой ребус на умножение ABC.

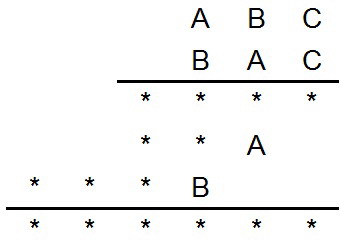
Восстановите в примере умножения отсутствующие цифры.

Ответ

286 × 826 = 236236

Решение задачи

Рассмотрим сначала произведение числа ABC на A (четвертая строка). Последняя цифра этого произведения - A, следовательно, она не 1, так как в противном случае и C было бы 1, но разные буквы по условию соответствуют неодинаковым цифрам. Замечаем также, что A не больше 3, так как в противном случае рассматриваемое произведение содержало бы более трех цифр, а в условии показано, что оно трехзначное. Следовательно, А может быть только числом 2, или числом 3. Пусть А=3. Каким должно быть С, чтобы ирон дение 3 на С оканчивалось цифрой 3? Этому услоиню удовлетворяет только С=1 (3*1=3). Но С не может бьиь единицей, так как произведение числа ABC на C - числи четырехзначное (третья строка). Следовательно, A не равно 3, но тогда А=2. Снова поищем С такое, чтобы произведение 2*С оканчивалось цифрой 2. Единственно возможное значение для С - число 6. Теперь рассмотрим произведение числа 2B6 на B (пятая строка). Последняя цифра этого произведения равна B; она же получается в результате умножения 6 на B. Для B возможны три значения: 4, 6 и 8, но 246*4=984 - число трехзначное, а произведение должно быть четырехзначным; значение 6 тоже отпадает (С=6). Следовательно, B=8. Итак, ABC=286 и BAC=826.

О задаче

Категория: Математические ребусы, Числовые ребусы,
Степень сложности: средняя.
Ключевые слова: ребус, умножение, цифра,
Источник: Математическая смекалка,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Удивительный цветок распустился посреди круглого пруда радиусом в 10 метров. Каждый день цветок удваивает свой диаметр и на 20-й день закрывает весь пруд. На какой день он закроет половину пруда?

a) 17
b) 19
c) 10
d) 15