Три брата.

В Кельне было три брата, имевших 9 сосудов с вином. Первый сосуд был емкостью в 1 кварту, второй содержал 2 кварты, и каждый следующий одной квартой больше, так что последний сосуд содержал уже 9 кварт. Требуется разделить вино поровну между тремя братьями, не смешивая содержимого сосудов.

Ответ

Решение показано на рисунке.

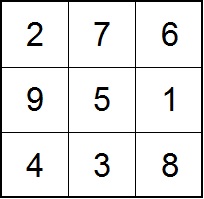
Решение задачи

Задача из немецкого рукописного сборника XIII века решается следующим образом: всего вина было ⁹⁽⁹⁺¹⁾/₂=45 кварт, следовательно, каждый брат должен получить по 45÷3=15 кварт. Задача сводится к определению числа комбинаций девяти чисел натурального ряда по три так, чтобы сумма всегда равнялась 15. Из этих девяти чисел, как известно, можно составить простейший магический квадрат (см. рисунок). Примем суммы, стоящие в вертикальных столбцах, за одно из решений. Так как братьев трое, то может быть шесть комбинаций. Но можно взять суммы горизонтальных столбцов. Тогда получим еще шесть решений, а всего, следовательно, 12 решений.

О задаче

Категория: Старинные задачи, Магический квадрат,
Степень сложности: средняя.
Ключевые слова: 3, 9, брат, вино, емкость, сосуд,
Источник: Сборник исторических задач по элементарной математике,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Пять школьников перед началом учебного года пошли в магазин, чтобы купить тетради. Первый из них имел 20 коп., второй 15 коп., третий 5 коп., четвертый 10 коп., а пятый 20 коп. Сколько тетрадей купили школьники на все имевшиеся у них деньги, если первый и второй вместе за их деньги получили в магазине 21 тетрадь?

a) 42 тетради.
b) 20 тетрадей.
c) 21 тетрадь.
d) 40 тетрадей.