Какова вместимость сосудов?

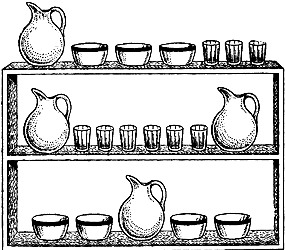
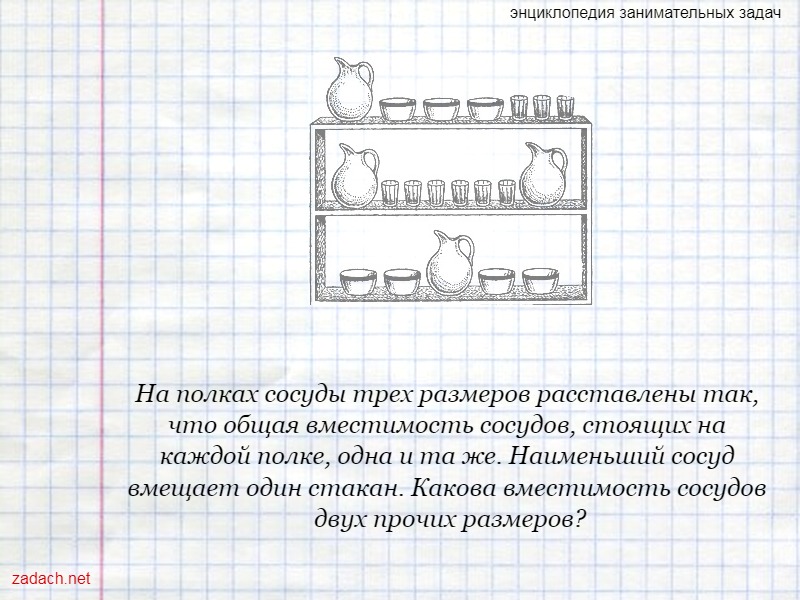
На полках сосуды трех размеров расставлены так, что общая вместимость сосудов, стоящих на каждой полке, одна и та же. Наименьший сосуд вмещает один стакан. Какова вместимость сосудов двух прочих размеров?

Ответ

Чашка равна 3 стаканам. Кувшин равен 6 стаканам.

Решение задачи

На основании рисунка составляем систему из трех уравнений, где V - общая вместимость одной полки:
1. Кувшин+3Чашки+3Стакана=V;
2. 2Кувшина+6Стаканов=V;
3. Кувшин+4Чашки=V.
Если вычесть из третьего уравнения первое получим: Чашка=3Стакана. Если из второго уравнения вычесть первое получим: Кувшин=3Чашки-3Стакана, с учетом предыдущего вывода: Кувшин=9Стаканов-3Стакана=6Стаканов.
Проверка:
1. 6Стаканов+9Стаканов+3Стакана=18 Стаканов;
2. 12Стаканов+6Стаканов=18 Стаканов;
3. 6Стаканов+12Стаканов=18 Стаканов.
Все верно.

Данную задачу можно решить без использования уравнений - логическим путем: сравнивая первую и третью полки, мы замечаем, что они отличаются друг от друга следующим: на третьей полке один лишний сосуд среднего размера, зато нет трех малых сосудов. А так как общая вместимость сосудов каждой полки одинакова, то, очевидно, вместимость одного среднего сосуда равна вместимости трех малых. Итак, средний сосуд вмещает три стакана. Теперь остается определить вместимость большого сосуда. Заменив на первой полке средние сосуды соответствующим числом стаканов, мы получаем один большой сосуд в 12 стаканов. Сравнив это со второй полкой, соображаем, что один большой сосуд вмещает шесть стаканов.

О задаче

Категория: Математические ребусы, Числовые ребусы,
Степень сложности: средняя.
Ключевые слова: 1, 3, кружка, кувшин, полка, сосуд, стакан, чашка,
Источник: Живая математика,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Сколько трехзначных чисел можно составить с помощью трех цифр 1, 2 и 3 так, чтобы одна и та же цифра встречалась в каждом числе не больше одного раза?

a) 8 чисел
b) 123 числа
c) 2 числа
d) 6 чисел