Две шестерни.

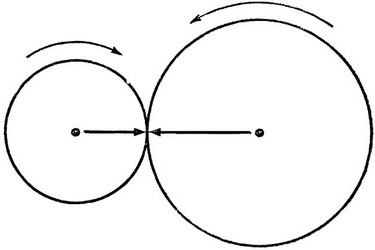
Две шестерни, на каждой из которых нарисовано по стрелке, находятся в положении, схематично изображенном на рисунке. Маленькая шестерня вращается по часовой стрелке до тех пор, пока стрелки на обоих шестернях не совпадут снова. Сколько оборотов успеет совершить маленькая шестерня до того, как стрелки совпадут, если число зубцов у большой шестерни равно 181?

Ответ

181

Решение задачи

Две находящиеся в зацеплении шестерни не могут вернуться в исходное положение до тех пор, пока на обеих шестернях через точку касания не пройдет некоторое число зубцов k. Число k есть наименьшее общее кратное числа зубцов каждой из шестерен. Пусть n - число зубцов меньшей шестерни. Из условия задачи известно, что у большой шестерни имеется 181 зубец. Поскольку число 181 простое, наименьшее общее кратное чисел 181 и n равно 181×n. Следовательно, прежде чем совпадут стрелки на обеих шестернях, меньшая шестеренка успеет совершить 181 оборот.

О задаче

Категория: Задачи с шестеренками,
Степень сложности: средняя.
Ключевые слова: 2, зубец, простое число, шестеренка,
Источник: Математические досуги,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Чайник вскипел, и только успели налить два стакана чаю, как от соседей прибежал мальчик. Он сказал, что сейчас по телевизору начнется интересная передача. Все, кто собирался пить чай, ушли к соседям. В каком из стаканов чай остынет скорее?

a) Остынут одновременно.
b) В стакане с ложкой скорее.
c) В стакане без ложки скорее.