|
|
Задачи про выстрел
Список занимательных задач про выстрел
Хороший стрелок стоит у одного борта.задача по физике
Хороший стрелок стоит у одного борта парохода, а у противоположного помещена мишень. Пароход движется в направлении, показанном на рисунке длинной стрелкой. Стрелок прицелился совершенно точно. Попадет ли он в цель?
Как определить среднюю дальность полета снаряда?старинная задача
Желая определить среднюю дальность полета снаряда из некоторого артиллерийского орудия, сделали 100 пробных выстрелов и нашли, что 18 выстрелов дали дальность 632 метра, 25 выстрелов дали дальность 628 метров, 53 выстрела дали дальность 620 метров, $4 выстрела дали дальность 640 метров. Какова средняя дальность?
Три охотника несколько дней подряд провели в тайге.занимательная задача
Три охотника несколько дней подряд провели в тайге на охоте. В последний день охоты утром случилась неприятность: переходя вброд небольшую речушку два охотника подмочили свои патронташи. Часть их патронов оказалась негодной к употреблению. Три друга поровну поделили между собой сохранившиеся патроны. После того как каждый охотник сделал четыре выстрела, у всех охотников вместе осталось столько патронов, сколько было после дележа у каждого. Сколько всего пригодных патронов было в момент дележа?
Пуля в часах.задача с часами
На рисунке вы видите циферблат часов, пробитый пулей из пистолета. Пуля попала точно в его центр, выведя часы из строя. Стрелки часов спаялись вместе, образовав одну прямую линию. Очевидно, они повернулись вокруг своей оси, поскольку не могли одновременно показывать на 3 и 9. Сколько было времени, когда пуля попала в часы?
На дереве сидело 10 птиц.задача с подвохом
На дереве сидело 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве?
На дереве сидели 5 ворон.задача с подвохом
На дереве сидели 5 ворон. Раздался выстрел, и две птицы упали. Сколько осталось ворон?
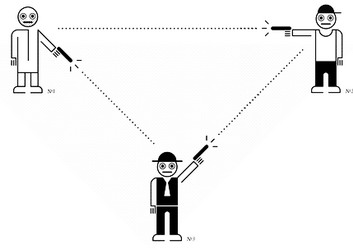
Дуэль трех лиц.логическая задача, задача на вероятность
Смит, Браун и Джонс, решив внести в обычную дуэль на пистолетах некоторое разнообразие, условились провести поединок по несколько измененным правилам. Вытащив жребий и узнав, кому из них выпало стрелять первым, кому - вторым и кому - третьим, они разошлись по своим местам, встав в вершинах равностороннего треугольника. Договорились, что каждый по очереди производит лишь один выстрел и может целиться в кого угодно. Дуэль продолжается до тех пор, пока не будут убиты любые два ее участника. Очередность стрельбы определяется только результатами жеребьевки и остается неизменной в течение всего поединка. Все три участника знают, что Смит никогда не промахивается, Браун попадает в цель в 80 % случаев, а Джонс, стреляющий хуже всех, промахивается так же часто, как и попадает в цель. Кто из дуэлянтов имеет более высокий шанс уцелеть, если считать, что все трое придерживаются оптимальных стратегий?
В какой точке земного шара находится путешественник?задача по географии
Путешественник находится в некоторой точке земного шара. Взглянув на юг, он обнаруживает в 100 м от себя медведя. Путешественник замирает на месте, а медведь проходит 100 м, двигаясь строго на восток. После этого путешественник направляет ружье точно на юг и стреляет в медведя. Спрашивается, в какой точке земного шара находится путешественник?
Оставить комментарий
Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.
Занимательные задачи
Ещё больше занимательных задач собрано в следующих разделах:
 Правило ложного положения |
 Решение задачи с конца |
 Правило (принцип) крайнего |
 Инвариант |
 Чётность |
 Старинные задачи |
|
|
|
|
|
| Энциклопедия занимательных задач | SirotaSOFT © 2021 - |