Ребус про моду.

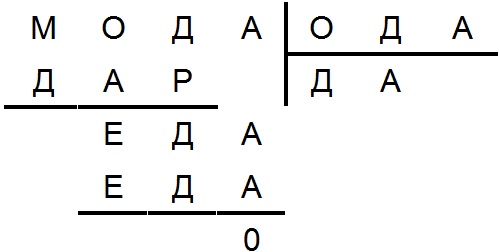
%Расшифруйте запись деления.

Ответ

3125 ÷ 125 = 25.

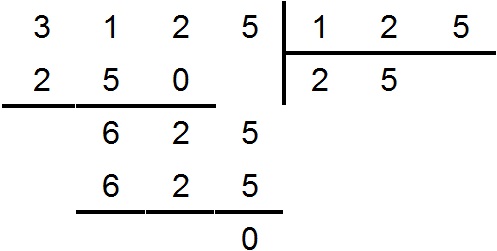
Решение задачи

1) ода × а = еда, и так как а, очевидно, не равно 1, то а = 5 или а = 6.
2) И при а = 5, и при а = 6 трехзначное произведение "еда" может быть лишь при о = 1.
3) При вычитании мод - дар = ед будем иметь: д - р = д, т. е. р = 0. И если теперь допустить,что а = 6, то е + а = е + 6 = 11 (так как о = 1), т. е. е = 5; но этого быть не может, ибо произведение ода × а = 1*6 × 6, начинающееся цифрой е, не может быть меньше 6**.
4) Значит, а = 5; из е + а = е + 5 = 11 получим: е = 6.
5) Цифра д - четная (так как ода × д = дар, т. е. а × д = 5 × д оканчивается цифрой р = 0).
6) д < 4 (иначе ода × а = 145 × 5 = 724 и окажется, что е = 7, а не 6). Но четное д ≠ 0 (так как р = 0). Следовательно, д = 2.
7) дар + ед = мод или 250 + 62 = 312, т.е. м = 3.

О задаче

Категория: Математические ребусы, Числовые ребусы,
Степень сложности: средняя.
Ключевые слова: деление, ребус,
Источник: Сборник задач по математике на сообразительность,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

Сколько спичек можно сделать из четырехгранного деревянного бруса (бревна), длина которого 10 метров, а ширина и высота по 1 метру, если длина спички 5 см., а ширина и толщина по 2 мм.?

a) 5 миллионов спичек
b) 1 миллион спичек
c) 10 миллионов спичек
d) 50 миллионов спичек