Числовой ребус с 8 на деление.

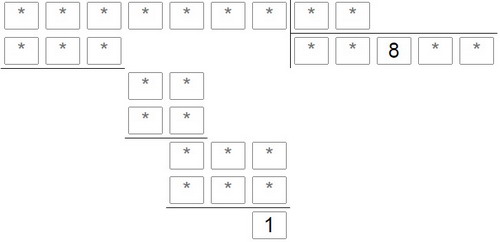
Восстановите в примере отсутствующие цифры, отмеченные звездочкой. Попробовать решить этот ребус онлайн можно по этой ссылке.

Ответ

Решение числового ребуса изображено на рисунке.

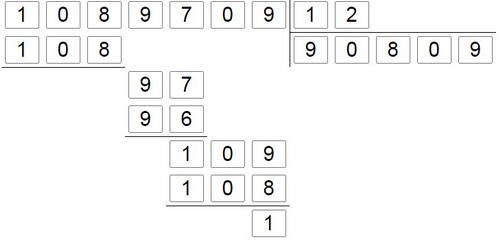
Решение задачи

Вот какой ход рассуждений приводит нас к цели: вторая цифра частного есть, конечно, 0. Это следует из того, что к остатку от первого вычитания снесена не одна цифра, а две: ясно, что после снесения первой цифры составилось число, меньшее делителя; а в таких случаях очередная цифра частного 0. По сходным основаниям заключаем, что четвертая цифра частного также 0. Всматриваясь в расположение кружочков, замечаем, что двузначный делитель, будучи умножен на 8, дает число двузначное; когда же его умножают на первую (пока неизвестную) цифру частного, получается число из трех цифр. Значит, эта первая цифра частного больше 8; такой цифрой может быть только 9. Сходным образом устанавливаем, что и последняя цифра частного - 9. Теперь частное определилось: 90809. Остается раскрыть смысл делителя. Делитель состоит, мы знаем, из двух цифр; кроме того, расположение кружков говорит о том, что это двузначное число при умножении на 8 дает также двузначное число; при умножении же на 9 оно дает произведение, состоящее уже из трех цифр. Что же это за число? Производим испытания, начиная с наименьшего двузначного числа - 10: 10 X 8 = 80, 10 X 9 = 90. Число 10, как видим, не удовлетворяет требуемым условиям: оба произведения двузначные. Испытываем следующее двузначное число - 11: 11 X 8 = 88, 11 X 9 = 99. Число 11 также, очевидно, не годится: оба произведения снова двузначные. Испытываем 12: 12 X 8 = 96, 12 X 9 = 108. Число 12 удовлетворяет всем требованиям. Нет ли еще таких чисел? Испытаем 13: 13 X 8 = 104, 13 X 9 = 117. Оба произведения трехзначные; следовательно, 13 не годится. Ясно, что неподходящими являются и все числа, большие чем 13. Итак, единственный возможный делитель - 12. Зная делитель, частное и остаток, легко находим делимое и восстанавливаем весь случай деления. Итак, делимое = 90 809 X 12 + 1 = 1089709.

О задаче

Категория: Математические ребусы, Числовые ребусы,
Степень сложности: сложная.
Ключевые слова: 8, деление, ребус, цифра,
Источник: Математическая шкатулка, Занимательная арифметика,

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

◄ На предыдущую страницу

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Решите задачу

На рисунке 17 шестеренок. Стрелкой указано направления вращения первой из них. В какую сторону будет вращаться последняя шестеренка (куда отклонится стрелка)?

a) Шестерни не смогут вращаться.
b) Против часовой стрелки (вправо).
c) Останется на месте.
d) По часовой стрелке (влево).